In the present chapter, we shall indulge in a closer scrutiny and frank criticism of Talmudic/Rabbinic hermeneutics.
1.Exposition and evaluation
Traditional presentations of the principles and practice of Rabbinic exegesis consist in listing the Thirteen Midot of R. Ishmael (at least, though other techniques may be mentioned, in contrast or additionally), describing roughly how they work, and illustrating them by means of examples found in the Talmud or other authoritative literature.[1]
Such an approach is inadequate, first of all, because the theoretical definitions of the rules are usually too vague for practical utility, and for purposes of clear distinction between similar rules. A simple test of practicality and clarity would be the following: if well defined, the rules should provide any intelligent person with a foolproof procedure, so that given the same database as the Rabbis, he or she would obtain the same conclusions as they did. The second important inadequacy in the traditional approach is the near total absence of evaluation; there are no validation procedures, no reductions to accepted standards of reasoning. There is no denying the genius of R. Ishmael and others like him, in their ability to abstract rules of intellectual behaviour from the observation of their own and their colleagues’ thought-processes in various situations. Nevertheless, as we shall see, their failure to treat information systematically and their lack of logical tools, yielded imperfect results.
We shall here propose some original ways to expose and evaluate Rabbinic hermeneutics (mainly, the 13 Midot). The most important step in our method is formalization; this means, substituting variable-symbols (like ‘X’ and ‘Y’) for terms or theses of propositions[2]. Formalizing an argument, note, means: formalizing all explicit and tacit premises and conclusions. The value of this measure is that it helps us to clarify the situations concerned, the Rabbinical responses to them, and the issues these raise. By this means, we move from a level akin to arithmetic, to one more like algebra. When we deal in symbols, we reduce immensely the possibility of warped judgment, due to personal attachment to some solution; all problems can be treated objectively. It should be said that logical formalization is not always the most appropriate tool at our disposal; in some cases, epistemological and/or ontological analyses are more valuable.
- We have two sets of data to thus formalize, or analyze in some manner: (a) the theoretical pronouncements of Rabbis (defining or explaining the rules, or guiding their utilization), and (b) the practical examples they give in support (illustrating or applying their statements). This work allows us to compare, and if need be contrast, Rabbinic theory and practice. As we shall see, they do not always match.
- Another utility of formalization or similar processes, is the possibility it gives us for comparing Rabbinic conclusions to the conclusions obtained by syllogism or other such established logical techniques. This is the ultimate goal of our study, to determine without prejudice whether or to what extent Rabbinic hermeneutics comply with deductive and inductive logic. As we shall see, they do not always parallel the course taken or recommended by ordinary logic.
In anticipation of such divergences, it is important to study the Rabbinic hermeneutic principles carefully, and distinguish between their natural factors and their artificial factors. The natural aspects are immediately credible to, and capable of formal validation by, ordinary human logic, and thus belong to secular epistemology. The artificial aspects, for which Rabbis claim traditional and ultimately Divine sanction, are controversial and require very close examination, for purposes of evaluation or at least explanation. Our task with regard to such additives is to consider whether the rationales for them offered by the Rabbis are logical and convincing, or whether these factors ought to be regarded as human inventions and errors.[3]
We shall in the rest of this chapter deal with the 13 rules of R. Ishmael under three large headings. “Inferences of information” – including rules 1-3, and 12, i.e. qal vachomer (a fortiori argument), gezerah shavah (inference by analogy), heqesh, semukhim, meinyano, misofo (contextual inferences), and binyan av (causal inference). Then “scope of terms” – including rules 4-7, referred to collectively as klalim uphratim (genera and species). Finally, “harmonization” – including rules 8-11, and 13, about which much will be said.
It should be clear that we have no intention, here, of masking any difficulties, but propose to engage in a “warts and all” exposé. The technicalities may be found hard-going by many people, but both secular and religious scholars, who endure through the ordeal, will be richly rewarded. They will find, not only an independent audit of Rabbinic hermeneutics, but a methodological demonstration of universal value. By the latter remark, I mean that the same method of exposition (by formalization) and evaluation (with reference to formal logic) can be applied to other movements of thought in Judaism, or outside it, in other religions or other domains (philosophy, politics, or whatever).
2.Inference of Information
We shall first consider the exegetic rules whose purpose is essentially to infer new information from passages of Scripture, rather than to elucidate or harmonize the text (the division is, admittedly, to some extent arbitrary). Included here are both deductive and inductive processes, of varying degrees of formality and certainty.
- We have treated qal vachomer (R. Ishmael’s Rule No. 1) in considerable detail already, and need only here remind of certain details. This refers to a natural thought-process, a fortiori inference, the most deductive form of Rabbinic argument. The Rabbis of the Talmud and those which followed them, although they had an exceptionally well-developed understanding of this form of argument, did not have a complete understanding of it, such as one might expect in the event of Divine revelation. Their knowledge of it was not formal; they did not clearly distinguish inductive and deductive stages of reasoning; they misconstrued certain applications of the dayo principle[4]; and they erroneously counted the number of a fortiori examples in the Tanakh.
It ought to be remarked that R. Ishmael’s formulation, just ‘qal vachomer’, is very brief – at best a heading; he does not define the processes involved. The distinction between miqal lechomer and michomer leqal is not given in the list of Thirteen Midot; I do not know whether it is explicitly found in the Talmud or only in later literature. To what extent were the Talmudic and post-Talmudic Rabbis aware of the difference between positive and negative a fortiori; did they ever note the distinction between copulative and implicational forms of the argument, did they use the secondary forms; at what point in history were the more complex Rabbinic formulations that we find in contemporary literature developed: these are all questions I ask myself, but have not researched the answer to. Historians of logic have still much work to do.
With regard to the legitimacy of the use of a fortiori argument. We validated four (or eight) primary moods, namely copulatives, subjectal or predicatal, positive or negative (and implicationals, antecedental or consequental, positive or negative) and a number of derivative secondary moods. Since the process has naturally valid moods, it follows that if these moods are used properly, no formal objection to their use in contexts not sanctioned by tradition is possible. Tradition can only restrict their use with reference to the inductive preliminaries (as we discussed under the heading of objections); but with reference to the purely deductive aspects, no Rabbinic legislation is possible[5]. It would be like trying to conveniently exempt oneself from the obligation of honesty or consistency!
The same freedom of thought must be acknowledged for all other purely deductive processes (or stages of processes), such as opposition, eduction, categorical or conditional syllogism, production, apodosis, and so forth. Any Rabbinic restrictions in such areas would be tantamount to an advocacy of antinomy, and cannot be tolerated. Rabbinic interference, on the grounds of some special Divine dispensation delivered at the Sinai revelation and transmitted by oral tradition, can only conceivably be applied to inductive processes; that is, with regard to situations which allow for more than one possible answers to a question, it is conceivable that there be a Divine decree as to which answer to favour in some specified situation(s) or all situations. However, we must keep in mind that the conceivability of such powers does not constitute proof that they exist in fact; it only makes logically possible a claim but does not justify it; and furthermore, that any controversy surrounding such powers throws doubt on their legitimacy.
- The technique of gezerah shavah (Rule No. 2) is also based on a natural thought-process, though a more intuitive and trial-and-error one. It consists in inference by analogy. The expression means “distinctive sameness”, and therefore refers to the fundamental epistemological processes of comparison and contrast, which are jointly the basic technique of all concept formation. Applying them to textual analysis, we would quite naturally (i.e. without need of special communication or dispensation of Divine origin) look for homonyms and synonyms, to understand the language used and its conceptual references. In all discourse, we may find labels used which are analogous (similar in root, if not identical words), and apparently have similar or various meaning(s) in different contexts; or we may find different labels used in different contexts, with apparently the same meaning intended.
The scientific-minded approach to gezerah shavah would run somewhat as follows. The meaning of a label, i.e. a word (every letter identical) or group of words (phrase), or word-root (having certain common consonants, in the same sequence; though possibly with some different vowels and consonants which indicate, on a wider grammatical basis, varying inflexions) or group of word-roots, is suggested by the various contexts in which it appears in the text(s) concerned, as well as in other texts and current usage, and through comparative etymology.
- Homonymy: If a, b, c... are all the occurrences of a label, and their assumed meanings (based on the above suggested methods) coincide, and no other assumed meaning(s) would be as coherent, then it may be assumed that the proposed single meaning is the intended meaning. If in some isolated context(s) the meaning of a label is uncertain, and it is coherent everywhere else, the same meaning can in all probability be generalized to the uncertain instance(s). But if the label is ambiguous elsewhere, there being one assumed sense in some contexts and some other sense(s) in others, then if no clear differentiating conditions are apparent, the sense most frequent elsewhere (if any) is the most probable, though some doubt remains.
- Synonymy: If A, B, C... are various labels and their assumed meanings (based on the above suggested methods) are unambiguous, and mutually identical or at least similar everywhere they occur, and not even conditionally dissimilar anywhere, then these labels may be considered to be equivocal and interchangeable; that is, they are different labels for the same thing. If in some isolated context(s) the meaning of a label is uncertain, and it is coherent everywhere else, the same meaning can in all probability be generalized to the uncertain instance(s).
Once the general meaning of a label or the equivalence of various labels is established, statements with the label(s) concerned may all be assumed to refer to the same subject-matter. A detailed example of the kind of analysis and synthesis here referred to may be found in our study of a fortiori in the Tanakh (JL 5-6).
A traditional example of gezerah shavah is given by EJ (with reference to Pes. 66a). The expression bemoado, meaning ‘in its appointed time’, is used both in Num. 9:2, concerning the Pascal lamb, and in Num. 28:2, concerning the daily offering (which includes the Sabbath); it is thence inferred that the Pascal lamb may be offered on a Sabbath (coinciding with Pessach), even though this entails activities forbidden on other Sabbaths.
It is obvious that such reasoning is highly intuitive and dependent on one’s overall context of knowledge. It is built up from the perception of words and the conception of their possible relations. The initial insights into possible meanings derived from immediate and wider context are conceptual acts dependent on the faculty of imagination; and subsequent ordering of the data, though a relatively mechanical process, is a function of the amount of data available at the time and taken into consideration. Such judgments can in no wise, therefore, be considered to have deductive value, but are eminently inductive.
With regard to Biblical text, we have little material to refer to, other than the document itself. This means that our conclusions are virtually pre-determined, since the data available are finite, even if they constitute a sufficiently large and varied sample of the Hebrew of the time concerned. Actually, sometimes a word or phrase is only used once in the whole document, and its meaning becomes a subject of conjecture; obviously the more often a label appears in the text, the more certain its meaning. With regard to Hebrew usage later in history, it is of course very significant[6], but it must be kept in mind that it has been and still is culturally influenced by the interpretations suggested by the Rabbis, and therefore it cannot necessarily be used to further justify those interpretations.
The natural interpretative process is adductive: an idea is floated, then tested in every which way for consistency[7]. It is, for this reason, susceptible to abuse. One may too easily stress similarities and ignore significant differences; and thereby stretch the application of an idea beyond its rightful borders. Or again, one may ignore similarities and emphasize incidental differences, and thus artificially restrict an idea. This is true of all argument by analogy; and repeated consistency-checking in an ever wider context of information provides the natural protection against error, as in all induction.
Now, such a relaxed and patient attitude can hardly be practical in a legal framework, where some decisive position may be required ‘right now’. On the other hand, the necessity to decide does not logically imply an impossibility to reverse the decision taken, later, in the context of new knowledge or modified conditions. The Talmudic authorities had debated matters and come to various conclusions which seemed wise to them. However, post-Talmudic authorities, intent on preserving these very decisions, proposed additional clauses to the hermeneutic principles which were to ensure they always resulted in the same conclusions, no matter how the data-context changed.
Thus, in relation to gezerah shavah, they claimed that the Sages were occasionally informed by tradition as to which topics were open to legal analogy, but left to find the verbal analogy which would justify it; or again, that the Sages were in some instances informed of words which could be used for such inference, but allowed to find appropriate circumstances for their use; or again, that the Sages were told in advance the number of valid gezerah shavah arguments there would be![8] Now, I find all that hard to believe. Not only because it is very surprising that such alleged ‘information’ is (apparently) not explicitly mentioned by the protagonists themselves, but only makes its appearance in writing centuries later; but because the transmission scenario itself is unreasonable.
Is it plausible that serious teachers would pass on vital legal information to their students in the form of riddles? Why would they engage in such games, and not get to the point, if they had the information? One cannot imagine a functioning law system in which it is not the law and its justifications which are transmitted from generation to generation, but conundra. For then, one would have to consider that the laws in question (i.e. those to be inferred by such means) had been inoperative until their formulation in the Talmud. In which case, surely, the more basic thesis that the law has gone on unaffected by time since Sinai – the very thesis these artifices were designed to defend – would be put in doubt. It seems obvious, therefore, that the above mentioned additional clauses are ex post facto constructs[9], based on no actual oral or written tradition.
The controversies surrounding yet other additional clauses to the gezerah shavah process, provide still more cause for suspicion that such additional clauses are not Sinai traditions, but later constructs (in this case, Talmudic)[10].
Thus, it is taught that the applicability of the gezerah shavah method depends on the ‘freedom’ of its middle term in one or both of its manifestations. This refers to whether each manifestation of the middle term involved, through which a legal factor is to be passed over from one issue to another, has already been utilized to justify some other Halakhah. Such a concern presupposes a principle that each unit of information in the Torah can only serve for one inference[11]; generic logic has no such restriction (a premise can be used in any number of arguments), but let us grant it to be a tradition. On this basis, three possibilities are considered: that the middle term is (a) ‘free on both sides’, (b) ‘free on one side only’, whether the source side or the target side, or (c) ‘free on neither side’. Authorities say and agree among themselves that a gezerah shavah inference of type (a) is irrefutable. With regard to type (b), some say it is always valid, while others regard it as conditionally valid. With regard to type (c), some regard it as conditionally valid, while others say it is always invalid.
Similarly, there is a debate as to how much legal detail a gezerah shavah allows us to pass over from premise to conclusion. There is also a debate as to whether once legal data has been transferred in one direction, other data may be transferred in the opposite direction, so as to equalize both sides, or whether the process is more restricted. It is irrelevant to us, here, which opinions are correct in these various debates – what is significant is simply the fact that there are at all disputes on matters so crucial.
Regarding the ‘freedom’ (mufneh) concept, an interesting remark may be added: it can be viewed as an attempt, albeit a rather primitive one, to express the sort of syllogistic reasoning which follows the drawing of analogies. The Rabbis ask: once a term A is seen as analogous to a term B (gezerah shavah), can the laws applicable to A be applied to B and/or vice-versa? Their answers by means of the ‘freedom’ concept may be understood as follows.
If both terms are ‘free’, it means that they were never before used in syllogistic inferences, presumably because they are both sui generis; consequently, the Rabbis assume them to be mutual implicants, and allow syllogism hither and thither between them. If only one is ‘free’, the Rabbis presume it to be a genus or species (I am not sure which) of the other, and thus allow syllogistic inference of laws from the genus to the species, though not vice-versa. If neither is ‘free’, it means that they have already led separate logical lives, so the Rabbis presume that the terms are unconnected (or at least that neither implies the other), and so avoid syllogistic inference.
This perspective explains the Rabbis’ concept, but does not fully justify it. For the basis of their syllogistic reasoning is too imprecise; they do not have a clear picture (even though this theory arose long after Aristotle) of the conditions of syllogistic inference. Similarity between terms and the histories of the use of such terms in inferences do not indubitably determine the implicational relations between these terms. The Rabbis lacked a clear understanding of opposition theory, as we shall see also in the section dealing with harmonization.
- We may, in my opinion, place under one heading, namely inference from context, the exegetic methods known as meinyano and misofo (Rule No. 12) and those known as heqesh and semukhim (regarded as part of Rule No. 2). All these take into account the textual closeness of an expression or sentence to certain other(s), and on this basis assume that there exists a conceptual relation between the passages under scrutiny, which makes possible an inference of certain attributes from the context to the expression or sentence. There is, we might remark, a small element of inference by analogy in such processes[12], though it might be characterized as extrinsic rather than intrinsic. The differences between these four techniques are, however, less clear (to me, at least).
An example of contextual inference: the Rabbis inferred (by the rule meinyano) that the commandment “thou shalt not steal” in the Decalogue (Exod. 20:13), refers to kidnapping, on the grounds that the two preceding commandments, against murder and adultery, are both capital offenses, and kidnapping is the only form of stealing subject to the same penalty (EJ, which refers to Mekh., Ba-Hodesh, 8,5).
This argument can be formalized as follows[13]:
|
(a) Murder is a capital offense |
A is E |
|
Adultery is a capital offense |
and B is E |
|
therefore (because textually adjacent) |
but C is next to A, B |
|
stealing is a capital offense |
therefore, C is E |
|
(b) but also, of the kinds of stealing, |
however, of all C |
|
only kidnapping is a capital offense |
only D is E |
|
therefore, as intended in the Decalogue, |
therefore, here |
|
“stealing” means “kidnapping” |
C means specifically D |
Thus, judging from this traditional example, inferences from context can be expressed to some extent in formal terms, their common property being a proposition like “C is next to...”. However, such argument has varying force, in view of the vagueness of the copula “next to”, and its inevitable irrelevancy in some cases (as I have argued, there has to be changes of topic).
Note that only (a) is contextual inference; (b) is an additional argument, which takes off from a foregone conclusion (of here unstated source) that kidnapping is a capital offense, and infers that the term stealing in the previous segment was intended to refer specifically to theft of people.
Meinyano seems to loosely appeal to the surrounding subject-matter without precise definition of its textual position relative to the passage at hand. Misofo refers to a later clause or passage for the information it infers; though as some commentators have pointed out, it could equally well refer to an earlier segment of text. In these two cases, the conceptual common ground of source and target text is to some extent evident. In the case of heqesh and semukhim, however, the inference is based almost purely on textual contiguity, the contiguous passages (within the same verse or in two adjacent verses, respectively) having little evident conceptual relation[14].
The natural justification of logistical inferences would be what we today refer to as ‘association of ideas’. When two ideas are placed next to each other in our thoughts, speeches or writings, it may be because of some logical relation between them, or entirely by accident, or again because one contains some incidental reminder of the other. This last possibility implies that in some cases, even when purely logical considerations are lacking, an inference might yet be drawn from the fact of proximity. However, the possibility of chance conjunction still remains: topic X may be entirely spent and the narrative moves on to topic Y, an entirely separate topic[15]. This alternative possibility means that inference based solely on position is tenuous. The Rabbis were apparently aware of this uncertainty, and would use such processes only as a last resort, when the verse being interpreted involved a doubt which they had no other way to resolve.
R. Ishmael did not mention the exegetic methods of heqesh and semukhim, and attempts by later authorities to explain this silence have a hollow ring. Thus, Bergman (with reference to the Sefer Hakerisus) says of R. Ishmael that “he regarded the hekesh as the equivalent of an explicitly written teaching”. If R. Ishmael did not even mention the subject, how can the later Rabbis know by tradition why he did not mention it. How can they have information on his thoughts on an unspoken issue? The very notion is self-contradictory: proving again that the authorities often confuse their personal assumption concerning some matter with a ‘received tradition’ (refusing to admit that R. Ishmael might not have known about these things, or that there might be no tradition concerning them, and that such issues must be resolved adductively).[16]
Again, R. Ishmael, apparently (and as the name given to the process implies), did not regard or was not aware that misofo inference was equally feasible in the opposite direction (‘mitechilato’, if we may say so), from an earlier to a later statement or clause. Later commentators (Bergman refers to Middos Aharon), who considered such reverse inference possible, explain R. Ishmael’s silence by claiming, effectively, that in cases where the solution precedes the problem, the inference is so obvious that listing it would have been a redundancy. That is another anachronistic argument, whether we agree with the validity of such inference in both directions or not. The commentators must admit the possibility that R. Ishmael did not hold the same opinion, or more likely still (since he himself does not mention it) that he just did not think of the issue at all!
- Inferences of the binyan av type (Rule No. 3) seem to be a Rabbinical attempt at causal inference – using the term ‘causal’ in its widest sense, including any mode of causality; i.e. not only natural-mode causation, of motion or change, but also extensional causality, of ‘static’ (i.e. class) differences, as well as logical causality, or rational explanation[17]. Causal inference has been much clarified in more recent times by John Stuart Mill[18], who identified the ‘methods of agreement and difference’. It results from observation of two kinds of events or things, such that the presence of one is always accompanied by the presence of the other, and therefore that the absence of the latter is always accompanied by the absence of the former. In such circumstance, one may, from observation of the first event or thing, presume the second even when it is not observable. This is an inductive process, involving analogy and generalization. Symbolically, broadly-speaking, the essential relation between a cause C and an effect E may be expressed by a hypothetical proposition and its contraposite:
If C, then E (and if not E, then not C).
However, the Rabbinical attempts at formulation of this natural principle stressed more the side of ‘agreement’ than that of ‘difference’. R. Ishmael refers to an inference ‘from one verse’ or ‘from two verses’. There were subsequently disputes as to the meaning of these subdivisions (which disputes, incidentally again tend to show the lack of a clear oral tradition). Some Rabbis understood them, respectively, as follows: if two topics (X, Y) have a certain feature (A) in common, then another feature (B) which the one (X) has may be assumed to be had by the second (Y)[19]; or, if three topics (X, Y, Z) have a certain feature (A) in common, then another feature (B) which two of them (X, Y) have may be assumed to be had by the third (Z). Other Rabbis claimed to understand R. Ishmael’s formula differently[20]. They sought for a common feature[21] (A, say) of topics under comparison (X, Y) which would explain their having in common some other property (B), in which case the reappearance of that same feature (A) elsewhere (in Z) could be taken as a sign of the same property (B) there (i.e. in Z). In fact, this formula is formally identical to the second of the above mentioned[22], merely adding the (valuable) comment that A is to be considered as the cause of B.
The difficulty in these statements is their emphasis on the positive, their attempt to generalize from a limited sample (X, or X and Y) without readiness to conceive the possibility of deviation from the apparently set pattern of conjunction (of A and B) in other cases, including, in particular, the case at hand (Y, or Z, respectively)[23]. Apparently sensing this weakness, the Rabbis tried to put a bit more emphasis on the negative, by pointing out differences in features between the (two or three) topics under scrutiny, thereby hoping to demonstrate other possible causes have been considered and eliminated. Thus, they might say, in the two-verse form of binyan av: X has C and Y lacks C, so that Z having C does not prove it has B; or again, X lacks D and Y has D, so that Z having D does not prove it has B. However, it should be clear that such statements are irrelevant to the main argument: they at best prove only that C or D do not cause B, but do not prove that A does cause B[24].
An example of binyan av, given in EJ (referring to B.M. 87b). The Rabbis attempt, with reference Deut. 23:25f., to determine whether a hired farm hand may eat produce, while working in fields other than those with vines or standing corn. To do so, they try to understand why the Torah allows him to eat in vineyards and in cornfields. They argue: it cannot be in relation to the obligation to leave gleanings for the poor (Lev. 19:10), since this applies to vine but not corn; and it cannot be in relation to the obligation to give the priest a portion of the dough (Num. 15:17-21), since this applies to corn but not vine; ‘therefore,’ it must be simply due to their being both plants, and the permission may be generalized to other produce.[25]
It appears from such redundancies that the Rabbis confused somewhat the trial and error mental process of looking for a cause (ratio cognoscendi), and the formal conditions of the objective causal relationship (ratio essendi). Had they known the latter clearly, they would rather have systematically first made sure they had a complete enumeration of the appearances of features A and B in the Torah, alone and/or separately, as well as their negations if any. Then, to make possible the inference from A to B, in situations where A is mentioned in the text but B is not mentioned, they would have to check, not only that A and B are sometimes both affirmed together (at least once, but the more the better), but also that A is never affirmed with an explicit denial of B (that is the missing negative element). Furthermore, the probability-rating of the inference would be proportional to the frequency of conjunction of A and B, compared to that of A mentioned alone without mention of B[26]. It is possible that in the cases where the Rabbis applied this principle, they (who knew the Torah by heart) automatically performed these consistency tests and probability judgments; but they did not always do so explicitly.
My analysis of binyan av suggests that the Rabbis often committed the fallacy[27] of post hoc ergo propter hoc (i.e. after this, therefore because of this). This consists in interpreting a sequence of events as causal, rather than merely coincidental, without proper justification. This kind of thinking is hard to avoid in the context of a closed book like the Bible. Because the characters and events in it seem exemplary and final, we are tempted to accept them as empirical data and generalize from them to our heart’s content, without regard to inductive rules. The Rabbis were conscious of the dangers of excess involved. For instance, that people might wish to imitate Pinchas, and kill out of some moral indignation[28]. In such contexts, the Rabbis would designate the event as somehow unique and limited to particular circumstances or to the time and place. The problem is of course that they were not consistently rigorous in their interpretations.[29]
It must be stated that aetiology does not insist that the cause be one event or thing, or that the effect be one event or thing; each of these (cause or effect) may itself be two or more parallel things or events, provided the stated rules of induction (agreement and difference) are adhered to for them all singly. Furthermore, if the rules of induction are not invariably adhered to (whether by a single event or thing or many of them), they might still be found to apply conditionally or compositely: that is, provided we manage to identify and distinguish the conditions under which our partial causes become complete causes or our occasional effects become constant effects[30]. Consequently, too, there may be circumstances in which one event or thing is the cause of a certain effect and other circumstances in which another is so; or again, a certain event or thing has some effect in one set of circumstances, and another effect in another set.
These details of causal logic were apparently not entirely understood by the Rabbis, judging from certain limiting suggestions they made. One such Rabbinic limitation was that (with reference to the symbols introduced above)[31] if X and Y have in common yet another feature (E, say) which Z lacks, then Z cannot be assumed to have B. I say, viewing ‘A+E’ as a joint feature, this objection seems reasonable; but it still remains possible that A causes B. Another Rabbinic limitation was the rejection of the possibility that distinct features of X and Y, such as C and D (see above), may independently cause B in their respective subjects, so that Z, which has only the common feature A, but neither of the distinct features C, D, may not have B. I say, it is conceivable that the two compounds ‘A+C+nonD’ and ‘A+nonC+D’ might be parallel causes, while the compound ‘A+nonC+nonD’ is not a cause: the issue depends on the negative side, which they ignored in their initial definition[32]. Such attempts at exception show, to repeat, that the Rabbis were not certain as to the precise conditions of causality[33].
There is a manifest failure of theoretical research in logic, independent of any Torah related doctrines, by the Rabbinic authorities. Consequently, as may be expected, there is a lot of controversy between them on methodological issues (which, of course, ultimately affect the law); and worse still, sometimes the controversy revolves around a totally artificial issue (which naturally enough emerges from some general belief to which the disputants are all attached). What amazes me is that the existence of such controversies does not cause any of the people involved to frankly question the ‘orthodox’ doctrine that the hermeneutic principles, in their entirety, are Sinaitic revelations.
A case in point is the discussion concerning the ‘two verses coming as one’ principle, according to which if a law L is stated in relation to two subjects, S1 and S2, and logically L(S1) implies L(S2), and/or vice-versa, so that one of the statements is redundant, then L may only be applied to the two situations specified. This principle has no natural basis, as far as I can see; i.e. it does not formally follow that L(S1) and/or L(S2) cannot logically imply some other, unstated application, say L(S3). If such implication does logically occur, it cannot be inhibited by Divine or Rabbinical fiat (God does not contradict His own natural laws, nor allow them to be by-passed by humans) [34]; for this reason, the restriction must be classed as artificial. Analytically, it seems to be merely an outcome of R. Akiba’s claim that there is no superfluous statement in the Torah; which idea is itself controversial, since R. Ishmael (theoretically) rejects it, claiming that the Torah speaks in the language of men. Whatever its source, there is controversy concerning the precise formulation of the proposed principle, from Mishnah onward. Some authorities (among them Tosafot) claim that at least two redundancies are required for such restriction. Some (among them Rashi) say that the restriction is in any case not general to all inference, but limited to attempts to extend the law concerned by means of binyan av inference. But I see no formal basis for these subjacent disputes, either.
The deep intellectual cause of such deviations from natural logic is, in my opinion, initially a naive non-formalism, gradually developing into a systematic anti-formalism (which is also naive, in other respects). The historical cause is an unfortunate, at first emotional and later ideological, antipathy to what they called ‘Greek knowledge’, which blocked any attempt to learn from the discoveries of others. For these people, logic has to adapt to the requirements of pre-conceived contents (the Halakhah), rather than all contents yielding to the dictates of an objective, formal logic. This Rabbinic claim of total control is evident, for instance, in Bergman’s statement in this context: “The rules regarding Scriptural texts... reveal a law only in relation to the place they are applied and not elsewhere”.
The doctrine of the Sinaitic origin of Rabbinic hermeneutics is not primary, but a derivative of the doctrine of the Sinaitic origin of Rabbinic law. The Rabbis thought they could manipulate logic however they saw fit, so long as they arrived at the required legal results. Controversies occurred only in relation to the necessity or efficacy of this or that manipulation, but not in relation to the underlying epistemological assumption.
These reflections need not be taken radically. Our concern, here, is with Judaic logic as such, not with Jewish law. If we throw doubt on the former, it does not necessarily follow that all, or any, of the latter is wrong; for, as logic teaches, denial of the antecedent (in this case, some aspects of Rabbinic hermeneutics), does not imply denial of the consequent (in this case, Rabbinic law) – unless their relationship happens to be exclusive. A law may be correct (i.e. truly Divinely-willed), but improperly derived from the text (i.e. from the wrong place or in the wrong manner). A law may, of course, alternatively, be incorrect, as well as improperly derived. These are not matters which can be dealt with in general ways; but each case must be reviewed carefully, after which the consistency of the whole must also be verified. In any case, logic cannot itself be made an issue of faith, something optional.
A statistical note. I have not so far found out just how many times each form of exegesis described here is actually used in the Talmud and other Rabbinic literature. For the moment, here is some information gleaned from the Index Volume of the Soncino edition (1952) of the Babylonian Talmud. As we saw in JL 5.5, this index contains some 137 references to qal vachomer argument (under various headings). With regard to various forms of argument by analogy, there are some 161 references (analogy, deduction by, 58; comparisons, for purpose of deriving laws, 1; gezerah shawah, 81; hekkesh, 17; semukin, 1; texts, proximity of, 2; textual reading, 1). Whether this index is complete, and whether each reference concerns a distinct sample or there are repetitions, and whether some references relate merely to theoretical discussions, I cannot venture to say[35].
Note also that we must distinguish between use of an argument: (i) within the Bible itself (e.g. we know of four or five cases of qal vachomer in the Torah, and two dozen more in the rest of the Bible); (ii) by the Rabbis, especially those of the Talmud, in their efforts of exegesis from the Bible, as a document, of Halakhic or Hagadic material; and (iii) by the Rabbis, especially post-Talmudic ones, in relation to the non-exegetic pronouncements of other Rabbis. Clearly, the statistical question constitutes a large and difficult research project in itself.
3.Scope of terms
Obviously, in the reading of any text, understanding the terms used is of the essence. This has two aspects: a qualitative aspect, which by its very nature presupposes knowledge of the language involved, and a quantitative aspect, which relates to determinations of scope. Rabbinic tradition has, of course, had much to say about both these aspects. The first aspect, elucidation of the denotations and connotations of terms, is in part dealt with within the hermeneutic principles, by way of inferences by analogy and context; and in part, it depends on cultural and religious tradition and the insights of commentators. The second aspect, concerning subsumptive issues, is covered by a set of hermeneutic principles which we shall now consider.
- The methods of exegesis known as collectively klalim uphratim[36], are efforts to interpret the effective subsumption of logically overlapping terms found in the Torah (and thence applicability of the proposition(s) involving those terms). Miklal uphrat (Rule No. 4) is the interpretation of a genus + species combination, in that sequence, as having a limiting effect, signifying ‘only the species mentioned’ (the species is mentioned for purposes of excluding others of the same genus); whereas miprat ukhlal (Rule No. 5) is the interpretation of a species + genus combination, in that sequence, as having an enlarging effect, signifying ‘the species mentioned and others like it’ (the species is mentioned as a sample of those in the genus). An easy way to remember these two rules is to say that the result is equal to the second of the two given terms. Other such rules, as we shall see, have an overall limiting result.
To put us into the picture let us note that, in everyday discourse, we would (depending on the precise wording) understand the conjugate scope of logically overlapping terms as follows, granting that G is an overclass and S1, S2... one or more of its subclasses, and that G and G’ are two classes which partly intersect without either subsuming all of the other’s instances and S, say, is the entire subclass referring to the G’ part of G. A statement whose subject is “GS” or “SG” would be interpreted minimally as concerning the species “S”[37], though in some cases the genus “G” might be appropriate. “G such as S1, S2...” might be read as “S1, S2...” (if ‘such as’ is taken to mean ‘similar to’) or as “G” (if ‘such as’ is taken to mean ‘for examples’). A listing of the form “S1, S2... indeed G” would likely be intended as “G”, though without a qualifier like ‘indeed’, a doubt might subsist. Lastly, “GG’“ or “G’G” is usually intended as “G and G’“ (i.e. “S”, their common ground), though occasionally might mean “G or G’“ (including both their grounds, as well as “S” or even possibly to the exclusion of “S”).
There is evidently much vagueness in ordinary language, which logical science can easily overcome by instituting conventions. This field of inquiry is not class logic proper, but a linguistic preliminary to it. Note that a mental act of ‘reconciliation of conflicts’ is involved, insofar as the terms dealt with are in some tension, according as we understand reference to a genus as concerning the whole of it (davqa) or most or an unspecified portion of it (lav davqa), and reference to a species as concerning it at least (lav davqa) or it exclusively (davqa). When the terms are mentioned together as subjects of propositions, there is therefore doubt as to whether the result is a generality, a contingency or an indefinite particularity. The logical rule, in case of doubt, is to acknowledge, by dilemmatic argument, the indefinite particularity (at least some) as true; deductively, we remain open-minded as to whether the generality (all) or contingency (some, but not all) is true; inductively, we opt for the generality, because it introduces no new polarity, unless or until conflicting evidence is found.
For the Rabbis, in the klal uphrat case, the genus is mentioned as a first approximation of the meaning intended, and the species is added to more precisely pin-point that meaning. For instance, in Lev. 1:2, “of the livestock (behemah), of the herd and of the flock,” the general term is one of variable connotation (it could be taken to include other types of animal, such as asses perhaps) and is clarified by means of the mentioned species. To explain why the species were not simply mentioned alone, without the genus, we are told that extensions unintended by the writer might then have been proposed, or alternatively that certain details suggested by the genus might have been missed; opinions differ among the authorities on this point. We could accept an amalgam of both as reasonable: the genus is there, effectively, to say “but do not include with these species, other dissimilar species of the same genus”.[38]
In the prat ukhlal case, some species are first listed to indicate the kind of thing intended, and the genus is added in conclusion to indicate “and other things of the same kind” to be also intended. For example, in Exod. 22:9, “an ass or an ox or a sheep, or any beast (behemah),” the species exemplify the things intended and the genus serves to extend the application of the law concerned to other similar things, implying the initial list not to be exhaustive. To explain why the genus was not simply mentioned alone, without the species, we are told that exceptions unintended by the writer might then have been proposed, or alternatively that certain details suggested by the species might have been missed; opinions differ among the authorities on this point. We could again accept an amalgam of both as reasonable: the species are there, effectively, to say “and be sure not to exclude from this genus, other similar species of the same genus”.
These methods, and other variations (mentioned below), are R. Ishmael’s; R. Akiba proposed others in the same contexts: he determined the scope of statements with reference to the principles of ribui umiut and miut uribui (amplification and limitation, and vice-versa). The technical difference between these approaches is essentially one of emphasis. Whereas in klal uphrat, the mention of species serves to more precisely define the initial genus; in ribui umiut, the explicit mention of species stresses the exclusion of certain dissimilar things, not explicitly mentioned, belonging to the initial genus. And whereas in prat ukhlal, the final genus serves to more broadly define the full extent of the list of species, adding to those explicitly mentioned more species not explicitly mentioned, while also incidentally somewhat limiting, as all definitions do, excessive extrapolations; in miut uribui, the mention of the genus stresses the limits of extrapolation more, excluding certain unmentioned species of it too extremely dissimilar to the mentioned species, while also incidentally suggesting certain unmentioned species to be included[39].
These forms of interpretation seem to me natural enough in themselves. In many cases, the wording is clear and no discussion is possible, anyway. However, in some cases, the results do not seem formally inevitable: one might sometimes view genus+species as signifying ‘genus, of which a sample species is...’[40], and species+genus as signifying ‘species, of which the relevant genus is...’[41]; in such cases, note, the term mentioned in second place is effectively in brackets, suggesting a proposition which communicates, in passing, some incidental information (not necessarily of immediate legal relevance). Consequently, if we take the rules as ex cathedra pronouncements, and attempt to always tailor our interpretations to fit their given formats, we are not unlikely to be occasionally misled. Clearly, behind such regulations is the rigid mode of thought which denies stylistic license to a document of Divine origin [42]
- With regard to the other combinations and permutations of these inferences of scope (classed as Rule No. 6), notably klal uphrat ukhlal and (apparently a later addition[43]) prat ukhlal uphrat, we need only add the following comments. These involve successive operation of the preceding two principles, with the klal stages having a broadening effect, and the prat stages a narrowing effect, the overall result being relatively narrow[44]. There is a proportionately greater opportunity to force the text into preconceived formats, rather than interpreting it naturally. It seems to me that we should always try to grasp the simple reading (pshat), and avoid deviation from it without overwhelming justification.
An example: Num. 6:3-4 forbids the Nazirite from drinking wine or strong drink or their vinegars or liquor of grapes, or eating fresh or dried grapes or anything made from the grapevine, from the kernels (chartsanim) to the husks (zag)[45]. According to Bergman, Nazir 34b reads this passage as prat ukhlal uphrat, but this seems to me unjustifiable, if ‘strong drink’ (shekhar, which can make one drunk) refers to alcoholic beverages other than wine and such. For in that case, ‘wine and strong drink’ cannot be wholly regarded as a prat in relation to ‘products of the vine’, which is a klal at best only in relation to wine and other grape-based drinks, fresh or dried grapes, and kernels and husks. The way all these items are listed is natural enough, in three classes grouping together alcoholic drinks (not all grape-based), normally eaten forms of grape, and parts normally wasted by the consumer, respectively, and additionally mentioning a wider class which most (but not all) of the items fall under. To insist on fitting them into the format prat ukhlal uphrat is artificial and inaccurate.[46]
- We should also mention here the principles miklal hatsarikh liphrat and miprat hatsarikh likhlal (general term requiring a particular [complement], and particular term requiring a general [complement]), which R. Ishmael’s list groups together as one (Rule No. 7)[47]. We may classify these, as Bergman does (presumably following previous authorities), with the klalim uphratim. The distinction between them is, he suggests, effectively: whereas klal uphrat and prat ukhlal and their ilk concern the collective effect of separately clear terms, the hatsarikh rules relate to vague terms whose precise meaning is only clarified by their mutual impact on each other. This distinction is very fine indeed, and rather forced judging by the examples given in the literature[48].
I would say, rather, that a case could be made for distinguishing between functionally independent terms (broadly speaking, classes of entities, which may however have a hierarchical relation; e.g., ‘animals’ and ‘bulls’) and dependent terms (more precisely, a relatively independent term, like ‘bulls’, and its complementary clauses; e.g. ‘the horns of’ or ‘the goring of people by’). The relation between independents is at best simply subsumptive (bulls are animals), whereas the relation between dependents is a more complex one, like possession or action (bulls have horns and bulls gore people)[49]. The former supplement each other, the latter complement each other. I do not mean to say that the Rabbis did classify their inferences under this or that heading on the basis of the distinction I am proposing (though perhaps they were trying to), but rather that if they insisted on making some kind of subdivision of the phenomena at hand, they might relatively usefully have selected it instead of the above mentioned[50]. I say ‘insisted’, because my distinction too is not radical enough to justify the formulation of additional hermeneutic rules. For one can usually (and much formal logic is based on this operation), perform what is known to logicians as a ‘permutation’[51], and change the complementary term into an independent one (bulls are ‘horn-having things’ and bulls are ‘goring things’).
A note on statistics. The Soncino general index has 77 references to the topic of klalim uphratim (supposedly, but I did not check). These come under various headings: amplification, 5; amplification and limitation, 15; amplification following amplification, 2; extension in exegesis, 5; general principles and exceptions, 1; general rulings, 2; generalisation, 2; generalisation and specification, 28; limitation in exegesis, 6; rule, general and particular, 1; rule, extension and limitation, 1; ribbui, 1; ribbui umiut, 1; specification, 1; specification as exegetical rule, 2; specification and generalisation, 4. As before remarked (in the discussion of Talmudic a fortiori), to what extent such a list is exhaustive and non-repetitive, is hard to say without further investigation. In any case, it does not tell us precisely how many times each rule is actually used.
4.Harmonization
Broadly put, the five remaining hermeneutic principles, Rules 8-11 and 13, which we shall label ‘harmonization rules’, serve to resolve apparent redundancies, discrepancies, doubts, tensions or inconsistencies between propositions. In some cases, their results are identical with those of formal logic; in some cases, they favour a course which is only a possibility among others according to formal logic; and in some cases, they suggest a course which formal logic would not have recommended. Note that these principles constitute units of thought-process, which may be operative individually in simple situations, or eventually successively in complex combinations.
Note that my formal analysis in this section is based on a possibly limited sample, drawn from the derivative literature on the topic that I have consulted. The few examples which are there presented as representative of the Rabbinic tradition may not be fully representative of that tradition. Furthermore, even if these examples are fully representative, it remains possible, indeed likely, that direct and thorough empirical research into the Talmud and other Rabbinic literature would reveal a much larger variety of forms of thinking, legitimate or not, in actual use[52]. The observations of the Rabbis of the past 2,000 years interested in these matters, and their conceptualizations and classifications of what they noticed, need not be taken for granted. On the contrary, as we show here, their failure to use formal methods make it very probable that they missed some of the available data and misjudged the data they had. Much work can still be done, and it is hoped that my initial efforts will be pursued further by others.
It should be noted that none of the harmonization rules here dealt with are mentioned in the Soncino index[53]. So, I have no inkling how often these rules are actually used in the Talmud.
Our interest here, note well, is not in the legal issues as such, but in the logical structure of the exegesis. I have no Halakhic ax to grind; my purpose is to institute a methodology for clarifying, classifying and evaluating Rabbinic exegesis, with reference both to its theoretical and practical aspects (that is, R. Ishmael’s rules and their explanation by Rabbis, on the one hand, and examples of their application in Talmud and other Rabbinic literature, on the other hand). Our empirical data consists of traditional pronouncements and actions, but our analytic approach to this data will be strictly objective and scientific.
We shall now deal with the first three (actually, four) of the hermeneutic principles which begin with the phrase kol davar shehayah bikhlal veyatsa... (Rules No. 8-10), which means literally ‘anything which was in a generality and came out...’[54]. Broadly put, in formal terms, these rules are concerned with the following exegetic situation:
|
Given: |
|
All S1 are P1 (major premise), |
|
and All S2 are P2 (minor premise), |
|
where All S2 are S1, but not all S1 are S2 (subjectal premise)[55], |
|
and P1 and P2 are in some relation f{P1, P2} (predicatal premise). |
|
What are resulting relations: |
|
between S1 and P1, and between S2 and P2, other than the above given; |
|
and between S1 and P2, and between S2 and P1 (conclusions)? |
This, then, concerns two subalternative subjects (S1 and S2, whose genus-species relation is defined in what we shall call the ‘subjectal premise’), which are found in Scripture separately related to two distinct predicates (P1 and P2, whose relation is defined in what we shall call the ‘predicatal premise’) [56]. The given relation of the genus (S1, the major subject) to its predicate (P1, the major predicate) will be called the major premise; while that of the species (S2, minor subject) to its respective predicate (P2, the minor predicate) will be called the minor premise. The question asked is, what information can be inferred concerning the various subjects and predicates (conclusions)? For us, this question is two-fold: (a) what conclusions does Rabbinic tradition propose, and (b) what conclusions does pure logic propose; comparing these sets, we might find them to coincide or intersect or entirely diverge.
The major and minor premises are given explicitly in Scripture (presumably, though it is conceivable that they be only implicit, provided they are derived from the text purely deductively). The subjectal premise may be textually given (or, again, strictly implied), or, as often happens, it may simply be obvious (natural knowledge); likewise, for the predicatal premise. The form of the latter relation, f(P1, P2), varies from rule to rule, and of course will affect the conclusions drawn. One of P1 and P2 may be subordinate to the other, or they may imply each other (being identical, or logically implicant); or P1 and P2 may be otherwise compatible (subcontrary or unconnected), or they may be incompatible (contradictory or contrary).
As for the ‘conclusions’ proposed, we shall see how they vary, and are generated, as we proceed; note that they may be inductive, as well as deductive. It should be remarked that in Rabbinic exegesis, one or more of the premises may be altered in the course of the argument: an initially general proposition may end up as contingent or as exclusive; such changes must be counted as ‘conclusions’ (or part of the overall ‘conclusion’), too.
Needless to say, the Rabbis never formulated their rules in such formal terms; I have expressed them in this manner to clarify them and evaluate them with certainty. R. Ishmael’s definitions (roughly, but passably) specify the major, minor and subjectal premises, as well as (though not always clearly) the putative ‘conclusions’, in ordinary language. But they do not specify, or do not more than hint at, the predicatal premises, which must be more or less guessed at, with reference to traditional examples; our hypotheses in this regard are confirmed by the symmetry and exhaustiveness of the combinations they postulate. As for logical evaluation, R. Ishmael and his contemporaries and successors do not make any effort at, or demonstrate any skill in, formal analysis of the processes; we will endeavor to fill the gap.
Furthermore, I very much doubt that these hermeneutic procedures were mechanically applied wherever their respective formal conditions were found; rather, I suspect, they were treated as a set of tools, which could be used, or ignored, as convenient, provided the Rabbis all approved. It is hard to imagine how they could proceed otherwise, because as we shall see the conclusions they draw are more often than not logically unnecessary (if not, in some contexts, illogical); whence it follows that inconsistencies are bound to arise in some cases, calling for a retreat from previous exegetic acts which caused the trouble. But to prove this prediction, one would have to study the Talmud in much more detail than I have done; ideally, one would need a well-ordered list of all the cases where exegesis took place.
Now, by means of syllogism, we can without further ado make the following inferences (side conclusions)[57]:
|
From the minor and subjectal premises, Some S1 are P2 (mood 3/AAI). |
|
From the major and subjectal premises, All S2 are P1 (mood 1/AAA). |
Yet other formal syllogisms may be possible, depending on the predicatal premise involved; such eventual inferences will be pointed out as we proceed.
In some cases, these various deductive inferences lead to no antinomy and are accepted by the Rabbis, though they may go beyond them and recommend some inductive process (for instance, an a-contrario reading or a generalization). In some cases, they lead to no antinomy, but are refused by the Rabbis (for reasons we shall see), who inhibit them in some way (for instance, by means of an anti-literal reading of the text or a particularization). In some cases, deductive logic from the given data results in a conflict, which must be resolved; and here again, the Rabbis may favour one reconciliation over another.
We have above considered, and will continue to do so, only the copulative forms of kol davar shehayah bikhlal; that is, forms involving categorical propositions. However, it should be clear that implicational forms of same are equally conceivable; that is, forms involving conditional propositions. Both types are used in Rabbinic examples, though perhaps the former more so than the latter. As shown below, the overall format of implicationals is similar to that of copulatives; all results are presumably the same, mutatis mutandis. We need not, therefore, treat both types; nor will we do so, to avoid repetitions. The significant difference between them is that, while copulatives involve four terms, implicationals involve four theses. Instead of the subjects (S1, S2) and predicates (P1, P2), we are concerned with antecedents (P1, P2 – not to confuse with the preceding symbols for Predicates; here P stands for Proposition) and consequents (Q1, Q2), respectively. Thus, for the record, we have, broadly put:
|
Given: |
|
If P1 then Q1 and If P2 then Q2 (major and minor premises), |
|
where P2 implies P1, but P1 does not imply P2 (antecedental premise), |
|
and Q1 and Q2 are in some relation f{Q1, Q2} (consequental premise). |
|
What are resulting relations: |
|
between P1 and Q1, and between P2 and Q2, other than the above given; |
|
and between P1 and Q2, and between P2 and Q1 (conclusions)? |
The common phrase “kol davar shehayah bikhlal veyatsa...” can now be interpreted more precisely. “Kol davar” refers to the minor term (S2); “shehayah bi-,” to the latter’s subsumption under the major term (S1, through the subjectal premise ‘S2 is S1’); “-khlal,” to the major premise (S1 is P1); and “veyatsa,” to the minor premise (S2 is P2). Note that in all these rules, the underlying subject is, normally, a person or persons (even if a beast, plant or mineral is ever mentioned, the ultimate subject, to whom any law might be addressed, is human). The effective predicate is clearly a law or set of laws, by which we must in this context understand some prescription, prohibition, permission and/or exemption. Let us now look at the hermeneutic principles concerned in detail.
- Rule No. 8 completes the said common phrase with the words ...min haklal lelamed, lo lelamed al atsmo yatsa, ela lelamed al haklal kulo yatsa. Translated literally, the principle states: “anything which was in a generality and came out of the generality, is to be taught: it is not to be taught ‘about itself, it came out’; but it is to be taught that ‘about the whole generality, it came out’”.
We may suggest the following interpretation: “A subject (S2), by virtue of its subsumption under another (S1), was included in a generality (All S1 are P1); then it (S2) was treated distinctively (All S2 are P2). In such case, the distinctive predicate (P2) is to be taught: do not just teach it (P2) with reference to the singled-out species (S2), but also teach it (P2) with reference to the whole genus (S1) [so that All S1 are P2]“. Thus, “atsmo” refers to the minor term (S2); “yatsa,” to the minor predicate (P2); and “haklal kulo,” to the major term (S1).
Although R. Ishmael’s principle itself does not specify the following point, judging by some examples given in the literature, the rule of lelamed concerns cases where the minor predicate P2 is subordinate to the major predicate P1. Thus, in this context, the predicatal premise undefined in our earlier general formula is:
All P2 are P1, but not all P1 are P2 (predicatal premise),
and the main conclusion apparently suggested by R. Ishmael is:
All S1 are P2 (main conclusion).
According to deductive logic, the said predicatal premise does not provide us with any additional inferences, other than the ones already obtained by other means (see above). Therefore, R. Ishmael’s suggested conclusion is at best inductive. Deductive logic allows that a genus may have a generic predicate and a species of that genus have a more specific predicate; it does not insist that the genus follows suit and have the more specific predicate, too. R. Ishmael, on the other hand, apparently considers that, with regard to the Torah, the minor premise, or more precisely, the implication of the minor and subjectal premises, ‘Some S1 are P2,’ has to be generalized to ‘All S1 are P2’.
The example, reported by Bergman, on which I based the above formalization is: Exod. 22:18 sentences a sorceress to death (generality), while Lev. 20:27 sentences a male or female medium or necromancers (“in whom is a ghost [ov] or familiar spirit [yidoni]“) to death by stoning (particularity); whence, granting mediums and necromancers to be included in the category of sorceresses (the textual basis for this subsumption is not given, note; also, commentators include sorcerers, arguing that the feminine is used only because most are women), it is inferred by such lelamed exegesis that sorceresses (of all kinds) are to be stoned. I noticed that the predicate change consists in adding a further precision (by stoning) to the original predicate (death sentence); and assumed this to be a sine qua non condition of application of this rule.
Note well that, according to natural logic, R. Ishmael’s suggested conclusion is not impossible (no antinomy ensues from it); it is just a non-sequitur (not formally inevitable). The minor premise’s implication is lav davqa, and may with equal possibility turn out to be general or contingent. Also, no redundancy would be involved in a davqa reading of ‘Some S1 are P2,’ contrary to R. Ishmael’s generalization, i.e. such that ‘Some S1 are not P2’. The suggested course is therefore an artificial one, recommended by a religious authority claiming Divine sanction. It is not essentially an inference, but a proposal that the minor premise not be read as exclusive.
Why the text did not simply say ‘All S1 are P2’ (instead of ‘All S2 are P2’) in the first place, if that is what it intended, is not explained; perhaps it would have been contextually inappropriate, suggesting false inferences from the surrounding context. Also, why the proposed inference is made, rather than reading the particularity as an exceptional provision, so that species of S1 other than S2 are not P2, though they are P1, is not explained. I would predict that the alternative reading of the particular, as a contingent, sometimes does occur in Rabbinic practice; but I have not searched for examples[58]. In any case, deductively, either outcome is formally acceptable; the proposed mood can only therefore be considered as an inductive preference, claimed as peculiar to Biblical exegesis.
- Bergman informs us that above is one version of the rule of lelamed, where the particular law teaches “about itself as well as the general law”. In another version, according to him, it teaches (not about itself but) “only about the general law”. From the example he gives, however, I would strongly disagree with his rendering of the latter version, while quite willing to grant that it exists in Rabbinic literature. But before discussing our differences, let me present this additional version in formal terms.
Let us first look at Bergman’s example. Lev. 22:3 sentences he who approaches holy offerings while impure to the ‘cut-off’ (excision, karet) penalty (generality); Lev. 7:20 sentences he who eats peace-offerings while impure to the same penalty (particularity); peace-offerings are listed as among other holy offerings in Lev. 7:37 (to be precise, this verse does not mention the general category of holy offerings, but only lists various kinds of offerings: burnt, meal, sin, guilt, consecration and peace). It is thence inferred that the consumption (or approach?) of offerings of lesser holiness than peace-offerings, such as those for Temple maintenance (Bergman does not specify where in the text this distinction in degree of holiness is established), are not subject to cut-off. [59]
Although neither R. Ishmael nor his successors specify the following point, judging by some examples given in the literature, the variant rule of lelamed concerns cases where the major predicate P1 is subordinate or identical to the minor predicate P2. Thus, in this context, the predicatal premise undefined in our earlier general formula is:
All P1 are P2 (predicatal premise),
and the main conclusion apparently suggested by Rabbis is:
Some S1 are not P2 (main conclusion).
Now, let us consider the syllogistic inferences we can make given this predicatal premise; there is only one, shown below. Notice that the result below is the same as the main conclusion of the original version of lelamed, except that here it is obtained by deduction, without need of an inductive extension.
From the major and predicatal premises, All S1 are P2 (mood 1/AAA).
Note that ‘All P1 are P2’ does not tells us whether all P2 are P1 or not all P2 are P1; either possibility is acceptable in the present variant, presumably. In the case where P1 and P2 imply each other (i.e. are identical or logically equivalent), nothing more can be deduced from the given premises.
There is a formal exception to the application of the second variant of lelamed, namely in situations where the rules of the klalim uphratim type are applicable. For the compound propositions ‘G and S are P’ and ‘S and G are P’, where S is subordinate to G, are each formally equivalent to a conjunction of the two simple propositions ‘G are P’ and ‘S are P’. And according to R. Ishmael, the conclusions to be drawn in these situations are, respectively, ‘Only S are P’ (davqa, by rule No. 4) and ‘All G are P’ (general, by rule No. 5). It follows that, when we come across subalternative subjects with the same predicate, we must first decide which rule is applicable. According to Rashi (Shevuot, 7a), the klalim uphratim rules would be used when the subalternative subjects are close to each other in the text (in the same verse), while the said variant of lelamed would come into play when the propositions are relatively far apart. The conclusion obtained is different from that of lelamed variant two, note well, in the case of ‘SG are P’; but in any case, the process as such is different even in the case of ‘GS are P’. Similar comments apply to other forms of klalim uphratim.
We thus see that, in this second variant of lelamed, the ‘conclusion’ postulated by the Rabbis, ‘Some S1 are not P2,’ is precisely the contradictory of the conclusion required by deductive logic (taking the premises at their face-value)! I am therefore very tempted to entirely reject this form of reasoning as antinomial. In any case, I would bet that this procedure is not invariably followed in the situation concerned, since it is very likely to lead to eventual inconsistencies; but I have not sought for demonstrative examples. However, we must try and understand what prompted the Rabbis to propose such twisted logic, and how it can be formally expressed.
Apparently, what prompted the Rabbis to opt for such a convolution, is the fact that the major predicate (P1) is less extended than the minor predicate (P2), or of equal extension, whereas the major subject (S1) is more extended than the minor subject (S2). Why would Scripture do so, rather than say ‘All S1 are P2’ in the first place, knowing that we could automatically draw such an inference? Therefore, the Rabbis supposedly reasoned, Scripture does not want us to draw such an inference.
With regard to logical means for such a position: granting the predicatal premise, which distinguishes this midah from the others and defines it, the only way we can prevent the conclusion ‘All S1 are P2’ from being drawn, is to deny the major premise, ‘All S1 are P1’. Note well that if we do so and say:
Some, but not all, S1 are P1 (particularization of major premise),
then the side conclusion that ‘All S2 are P1’ no longer follows, and the relation between S2 and P1 remains problematic.
Objections which can be raised to this Rabbinical position are the following. If the Rabbis are surprised in the present case that the text did not immediately say ‘All S1 are P2,’ why were they not equally surprised in the previous case that the text did not directly say it, if that was its intention?
Furthermore, in the case where P1 is subordinate to P2, there could be a contextual reason for giving the major premise a more specific predicate, to avoid some unwanted inference (such as a first variant lelamed from another minor premise) which could otherwise be drawn from a generic predicate. In the case where P1 and P2 are one and the same, the Rabbinical surprise can only be due to the different extensions of the subjects, S1 and S2; here again, a contextual explanation could be adduced: it is conceivable that undesirable inferences might have been drawn from a misplaced generic subject or specific subject.
God, the writer of the Torah, may have thought: ‘I can allow Myself such wording, since the Rabbis will recover My final intention eventually anyway, by syllogism through the predicatal premise.’ The mere facts that the text is considered as written by a conscious Being and that syllogism is easy, does not prove that God intended what the Rabbis say He intended. An alternative course is sustainable, so their discomfort with the apparent redundancy was not justified. So much for evaluation; let us go back to description.
In the new variant of lelamed, the putative ‘conclusion’ denies the major premise. It is not a deduction (since in deduction, a conclusion can never contradict a premise), nor a particularization in reaction to textual inconsistency (since there was no contradiction between the premises, no conflict calling for reconciliation). Strictly-speaking, therefore, it cannot be called an inference, but at best a reading motivated by a vague discomfort with the logistics of the text. The Rabbis arbitrarily (without formal motive) reject literal reading of the major premise, ‘All S1 are P1,’ and tell us that it is not davqa general, but really contingent. Their alleged conclusion, that ‘Some S1 are not P2,’ is the cause, rather than the effect, of such reading. The anti-literal reading becomes necessary to prevent absurd consequences, only once the desired ‘conclusion’ has been artificially chosen; furthermore, that ‘conclusion’ does not necessarily follow such reading, it is only made possible by it.
Thus, the second variant of lelamed ends, rather than starts, with particularization of the major premise; no process is involved in getting to its main conclusion. Note that, in this context, the syllogistic inference from the original major premise (All S1 are P1) and the supposed predicatal premise (All P1 are P2), namely ‘All S1 are P2’, is Rabbinically interdicted.
It follows incidentally, from the main ‘conclusion’, as the Rabbis claim, that ‘there is at least one species of S1 unlike S2, call it S3, which is not P2’; i.e. that the minor predicate is applicable only to the minor subject (and eventually others like it); the trouble with this eduction, however, is that it adds no concrete knowledge, since it cannot tell us in what respect other species are ‘like’ or ‘unlike’ the given species[60]. In effect, then, though the minor premise as such (All S2 are P2) remains unaffected, it becomes exclusive:
Only S2 are P2 (additional conclusion).
Note well that this exclusive proposition is not formally required as such, but is approximately true granting some leeway for the subject to expand somewhat (i.e. ‘S2’ here may include other species of S1 like S2, but in any case excludes some species of S1 unlike S2). The syllogistic inference that ‘Some S1 are P2’, from the minor premise and the subjectal premise (All S2 are S1), remains valid; and is of course to be conjoined to the Rabbis’ conclusion ‘Some S1 are not P2’, to form a contingent proposition.
To repeat, the proposal of the Rabbis is logically untenable, unless we doctor the premises in a convenient manner. To prevent contradiction, the major premise ‘All S1 are P1’ has to be denied, i.e. particularized to ‘Some, but not all, S1 are P1’. However, this measure does not result in the desired main ‘conclusion’ being inferred deductively; it remains a ‘foregone conclusion’ (a thesis without justification in the premises, old or new). All that the adjustment of the major premise does, is render the main ‘conclusion’ formally conceivable; its preference by the Rabbis remains an inductive act. This act would be acceptable to science, if put forward as a tentative hypothesis to be tested by other data; however, pronounced as a fixed fiat, not open to review, it becomes, from the scientific point of view, an arbitrary act. The Rabbis, of course, claim Divine sanction for it; but we must point out that such a claim is not verifiable by scientific means. We shall leave the matter at that and move on.
We can now return to criticism of Bergman’s formulation. The distinction between the two variants of lelamed which he proposes is incorrect. In the first variant, we could, indeed, say that the particular law teaches “about itself as well as the general law,” insofar as the minor predicate is Rabbinically applied to the major subject. However, it cannot be said, in the second variant, that the particular law teaches (not about itself but) “only about the general law”. The particular law is in fact unaffected by the process, and the general law does not come to resemble it. The best we can say is that the particular law is viewed by the Rabbis as an exception to the general law; it makes the latter cease to be general. The minor predicate is reserved for the minor subject (and others eventually ‘like’ it), and other members of the major subject (‘unlike’ the minor subject) are deprived of the minor predicate.
Let us see, now, how we would have to interpret R. Ishmael’s lelamed formula, so that it covers the second variant. To adapt the sentence “kol davar shehayah bikhlal veyatsa min haklal lelamed lo lelamed al atsmo yatsa ela lelamed al haklal kulo yatsa”, we must read into it something to the effect that “A subject (S2), by virtue of its subsumption under another (S1), was included in a generality (All S1 are P1); then it (S2) was treated distinctively (All S2 are P2). In such case, the distinctive treatment (All S2 are P2) was intended to teach us something. It was not done just to teach us something about itself (S2) that the species was differentiated (in All S2 are P2), but also to teach us something [else] about the whole genus (S1) from which it was differentiated [namely, that Not all S1 are P2]“.
In this modified version, we read the implicit word “else,” meaning “other than the distinctive treatment,” into the formula, so that the ‘conclusion’ be different for the genus than it was the species. Here, “yatsa” refers to the whole minor premise, rather than to the minor predicate, note.
Thus, we might distinguish the two variants of lelamed, by labeling the first “lelamed oto hadavar leshar haklal” (teach the same thing, P2, with regard to rest of the genus, S1), and the second “lelamed hefekh hadavar leshar haklal” (teach the opposite thing, notP2, with regard to the rest of the genus, S1). Compare this to Bergman’s differentiation, “as well as the general” and “only the general,” and you can see that he was inaccurate.
Let us now review the technical similarities and differences between these two versions of lelamed, other than their common grounds with the other rules of the type kol davar shehayah bikhlal veyatsa. (a) In both, the predicatal premise, which serves as the distinctive condition to application of the rule, asserts implication between the predicates; however, in the first version, which we have called lelamed oto hadavar, the minor predicate is subordinate to the major predicate; whereas in the second version, called lelamed hefekh hadavar, the major predicate implies the minor predicate. (b) The main conclusion of the first is general positive (All S1 are P2), while that of the second is particular negative (Some S1 are not P2); they agree, however, that Some S1 are P2.
Finally, (c) they involve distinct thought-processes: lelamed oto hadavar proceeds by inductive generalization of a particular implication of the minor premise (viz. Some S1 are P2), whereas lelamed hefekh hadavar proceeds by arbitrarily postulating a conclusion contradictory to an implication of the major premise (viz. All S1 are P2) and consequent reconciliatory particularization of the major premise itself. Neither process is called-for or necessary according to natural logic, neither constitutes deduction from the predicatal premise which prompts it; but the artifice involved in the former is relatively straightforward, while that involved in the latter is more twisted.
In view of the similar predicatal premises, the traditional classification of lelamed hefekh hadavar with lelamed oto hadavar seems sound. But at the same time, in view of the radical differences in process and conclusion, we may well doubt that the second variant was intended in the original definition of R. Ishmael. I suspect its formulation was a later development, even if it was used unconsciously earlier. It could equally well have been instituted as a distinct rule of the kol davar shehayah bikhlal veyatsa type. It resembles the rule of the liton toan acher, shelo kheinyano type (see below) in that it involves a particularization of the major premise, though for quite different reasons.
The next two rules (Nos. 9 and 10) continue the common phrase kol davar shehayah bikhlal veyatsa... with the words ...liton toan acher. We shall now analyze these.
- Let us first deal with Rule No. 10, which is easier. It completes the preceding clauses with the phrase ...shelo kheinyano, yatsa lehaqel ulehachamir, and may be translated literally as “anything which was in a generality and came out to posit another thesis, which is incompatible, came out to lighten and to harden”. The expression ‘shelo kheinyano’ tells us that the major and minor predicates are, by their very nature (or by virtue of some other part of the text, perhaps), incapable of conjunction in one and the same subject. They are not merely different, but mutually exclusive; there is a radical cleavage between them.
Thus, although neither R. Ishmael nor his successors specify the following point, judging by some examples given in the literature, the rule liton toan acher, shelo kheinyano concerns cases where the major predicate P1 and the minor predicate P2 are contrary or contradictory. Thus, in this context, the predicatal premise undefined in our earlier general formula is, minimally:
No P1 is P2 (and No P2 is P1) (predicatal premise).
Note that this gives a minimal definition of the incompatibility between P1 and P2 referred to. The bracketed clause is redundant, being implied anyway. In the case of contradictories, we must additionally say: No nonP1 is nonP2 (which implies No nonP2 is nonP1). While in the case of contraries, we must add: Some nonP1 are nonP2 (which implies Some nonP2 are nonP1).
A comment should be made here regarding compound predicates. If one predicate X consists of two concepts a + b, while the other predicate Y consists of only one of these concepts (say, a), without mentioning the other (b), then three readings are possible[61].
- X = ‘a + b’ and Y = ‘a + b’ or ‘a + notb’. Here, knowing that either event may actually occur; the result is that X is included in Y, or in other words, Y is a genus of X (as well as of some other species, Z = a + notb). Therefore, we would apply the rule lelamed; opting for the variant hefekh hadavar if P1=X and P2=Y, or the variant oto hadavar if P1=Y and P2=X.
- X = ‘a + b’ and Y = ‘a + b’. Here, we have generalized factor ‘b’ from the ‘a’ in the case of X, to ‘a’ in all cases, including that of Y; the result is that X and Y are identical. Therefore, whether P1=X and P2=Y, or P1=Y and P2=X, we would apply the rule lelamed hefekh hadavar.
- X = ‘a + b’ and Y = ‘a + notb’. Here, we have generalized from the non-mention of ‘b’ with regard to Y, to the actual absence of ‘b’ in Y; the result is that X and Y are incompatible[62]. Therefore, whether P1=X and P2=Y, or P1=Y and P2=X, we would apply the rule shelo kheinyano.
Often, as Bergman acknowledges, Scripture displays a discrepancy, not by commission (assigning incompatible predicates to subalternative subjects), but by omission (as just described). As the above analysis shows, in the latter case, before we can apply one of the hermeneutic rules, a decision process must be followed[63]. Thereafter, if the compounds involved are found incompatible, we apply shelo kheinyano; otherwise, one of the variants of lelamed. It is noteworthy that the rule shehu kheinyano, as defined further on, never comes into play in this context![64]
Now, let us consider the syllogistic inferences we can make given the said predicatal premise, ‘No P1 is P2’:
|
From the minor and predicatal premises, No S2 is P1 (mood 2/EAE), |
|
From the major and predicatal premises, No S1 is P2 (mood 1/EAE). |
No additional inference is possible with the additional clause (No nonP1 is nonP2) of contradictory predicates, nor with that (Some nonP1 are nonP2) of contrary predicates, note. Now, comparing these new results to the implications of the major and minor premises in conjunction with the subjectal premise, namely ‘All S2 are P1’ and ‘Some S1 are P2’, we see that they are respectively contrary and contradictory propositions. Thus, if, in the text, we come across subjects in a genus-species relation which have incompatible predicates, we are facing a situation of formal inconsistency. This is not an antinomy due to a Rabbinic interpretation, but one inherent in the text, note well. A formal resolution of the conflict is absolutely required.
It is a principle of inductive logic that harmonization is to be sought by effecting the minimum retreat from generalities, necessary to restore consistency; this is the most likely outcome[65]. If it can be shown that the subjects are not subalternative and/or that the predicates are not incompatible, we are of course no longer in the same situation and some other process may be appropriate. But, granting that the subjectal and predicatal premises are correct, the only way to achieve the required result is to particularize the major premise. With regard to the minor premise, if it is particularized alone, a conflict remains; it may of course also be particularized, but that does not affect the result. That is, logic indisputably demands that:
Some, but not all, S1 are P1 (resolution of conflict, leading conclusion).
The proof of what we have just said will now be presented:
- If we particularize only the minor premise, so that ‘Some, but not all, S2 are P2’, and we keep the major premise, then the following sorites remains possible: ‘All S2 are S1’ (subjectal) and ‘All S1 are P1’ (major) and ‘No P1 is P2’ (predicatal), therefore ‘No S2 is P2’; but the latter conclusion disagrees with ‘Some S2 are P2’ (from minor); therefore, we still have an inconsistency.
- On the other hand, if we particularize only the major premise, so that ‘Some, but not all, S1 are P1’, and we keep the minor premise, then the following sorites remains possible: ‘Some S1 are S2’ (converse of subjectal) and ‘All S2 are P2’ (minor) and ‘No P2 is P1’ (converse of predicatal), therefore ‘Some S1 are not P1’; and the latter conclusion agrees with ‘Some, but not all, S1 are P1’ (altered major); therefore, this measure resolves our contradiction.
- If we particularize both premises, no such sorites can be constructed. The results are equally acceptable; but this measure involves a more radical reaction than necessary, it goes beyond logical necessity. Thus, the minor premise might or might not be denied; what counts is denial of the major premise. The difference in behavior is due to the minor term being narrower than the major term.
That is, we must say that the text, which at first sight led us to believe ‘All S1 are P1’, was not intended to be taken literally, but only to suggest that ‘a great many, perhaps most, but not all’ of S1 are P1. The syllogistic consequences of this new result on the relations between S1 and P2 and between S2 and P1 are as follows.
|
From the minor and subjectal premises, Some S1 are P2 (3/IAI). |
|
From the major and predicatal premises, Some S1 are not P2 (1/EIO). |
|
From the major and subjectal premises, no conclusion (1/IA?). |
|
From the minor and predicatal premises, Some S2 are not P1 (2/EIO). |
The latter consequence is true whether the minor premise is particularized or not. If the minor premise is not particularized, we can moreover infer ‘No S2 is P1’; if, however, it is particularized (for independent reasons, for we have here no reason to do so), then whether ‘No S2 is P1’ or ‘Some S2 are P1’ remains an open question, formally. These consequences, together with the altered major premise (Only some S1 are P1), constitute our conclusions, according to formal logic. Now, let us turn to the Rabbis, and see what they say.
An example of liton toan acher shelo kheinyano given by Scherman: Exod. 21:2-6 presents a set of laws relating to the release of a Hebrew slave (eved ivri, this is taken to refer to a thief sold by the courts to repay his theft, as per Exod. 22:2; for the self-sold poor, see Lev. 25:39-43); then Exod. 21:7-11 presents a very different set of laws for the release of a daughter sold as maid-servant (amah); conclusion, the initial set was for male Hebrew slaves only, and the laws of each group cannot be applied to the other group.[66]
Thus far, the formal conclusions apparently suggested by R. Ishmael are identical to those of natural logic, in the present rule. However, the above example suggests that the Rabbis take a more definite position and additionally conclude:
No S2 is P1 (additional conclusion).
Whether the Rabbis invariably go that far, or only occasionally, I cannot say without a full list of examples; but offhand, it seems pretty typical. This conclusion can be due to either of two policies. Either the Rabbis consider that the minor premise ought to be kept general, i.e. as ‘All S2 are P2’; in which case, the said additional conclusion follows from the minor and predicatal premises deductively. Or the Rabbis consider that the minor premise ought to be particularized; in which case, their arrival at the additional conclusion is due to a generalization from the implication ‘Some S2 are not P1’ of the minor and predicatal premises. The first alternative is preferable to formal logic, in that no unnecessary doctoring of given data is involved. The second alternative, if used by the Rabbis, would constitute an inductive act (regarding which we can reiterate the remarks previously made in similar circumstances; namely, that such an act is arbitrary, if presented as a fixed rule; though scientifically acceptable, if presented as a tentative hypothesis).
- Rule No. 9 completes the common phrase kol davar shehayah bikhlal veyatsa... with the words ...liton toan acher, shehu kheinyano, yatsa lehaqel velo lehachamir, and may be translated literally as “anything which was in a generality and came out to posit another thesis, which is compatible, came out to lighten and not to harden”. The expression ‘shehu kheinyano’ is at first unclear; but we can arrive at its intended meaning by a process of elimination. ‘Shelo kheinyano’ (see rule No. 10, above) clearly refers to an incompatible predicate; so, ‘shehu kheinyano’ must refer to some kind of compatible predicate; however, it cannot refer to a minor predicate which subalternates or mutually implies or is subalternated by the major predicate, as such relations have already been treated under the headings of lelamed; therefore, ‘shehu kheinyano’ must specifically refer to a subcontrary or an unconnected predicate. That is, here, though the two predicates are by their natures different, in the sense of distinguishable, they are not mutually exclusive, but conjoinable.
Traditionalists may not agree with this definition of shehu kheinyano. They might distinguish it from shelo kheinyano, by saying that both concern somewhat divergent predicates, the former’s are ‘of similar subject-matter’, while the latter ‘of different subject-matter’, or something to that effect. But such a distinction is of little practical value, because it is difficult to determine by its means what is “different, but not very” and what is “very different”; the distinction in practice becomes pure guesswork, or (they might say) a matter of ‘oral tradition’.
Though I try my best, I see no way to enshrine such a distinction in formal terms. It cannot, for instance, be ascribed to the issue of compound predicates (see above). A genetic explanation may be the relation between two degrees of a concept X, say X1 and X2, and an incompatible of it, say Y (implying nonX): we could say that the greater X (X2) is further than the lesser X (X1) to nonX (considered as X=0); but both X1 and X2 remain in conflict with Y. The notion of “less” or “more” incompatible is, strictly speaking, a mixed bag. For formal logic, all incompatibilities are equivalent, without degrees; things either cannot coexist, or they can coexist (under certain conditions).
The examples which commentators usually give for the two processes are clearly identical from a formal point of view: substitute symbols for the terms, and you will see that the predicates are formally incompatible in both sets of examples. It follows that there is no way to justify different procedures for the two situations. Furthermore, if both rules of liton toan acher indeed referred to incompatible predicates, then R. Ishmael’s hermeneutics would be short of a comment on compatibles (in the sense, unconnecteds or subcontraries).
Thus, although neither R. Ishmael nor his successors specify the following point, we can say that the rule liton toan acher, shehu kheinyano concerns cases where the major predicate P1 and the minor predicate P2 are unconnected or subcontrary. This hypothesis is based on the said process of elimination, and hopefully will eventually be confirmed by some examples given in the literature. In this context, then, the predicatal premise undefined in our earlier general formula is, minimally:
|
Some P1 are P2 and some P1 are not P2, and |
|
(some P2 are P1 and) some P2 are not P1 (predicatal premise). |
Note that this gives a minimal definition of the sort of compatibility between P1 and P2 referred to. The clause ‘Some P1 are P2’ serves to eliminate incompatibilities, which are dealt with under the heading of shelo kheinyano; the bracketed clause ‘Some P2 are P1’ is implicit in it, and so could be left out. The clauses ‘Some P1 are not P2’ and ‘Some P2 are not P1’ serve to eliminate implicational relationships, which are dealt with under the heading of lelamed. In the case of subcontraries, the clause ‘All nonP1 are P2’ (which implies ‘All nonP2 are P1’) would have to be added; in that case, the clauses ‘Some P1 are not P2’ and ‘Some P2 are not P1’, being both implied by the larger clause, could be left out. In the case of unconnecteds, the clause ‘Some nonP1 are not P2’ (which implies ‘Some nonP2 are not P1’) would be added, instead.
Now, let us consider the syllogistic inferences we can make given the said (compound) predicatal premise. In conjunction with the major premise, all we can formally infer is that Some P2 are not S1 (mood 2/OAO). However, this information tells us nothing of the relation of S1 to P2 (in that order), other than what we already know from the minor and subjectal premises, viz. that Some S1 are P2 (which is indefinite, note). Similarly, we can infer, from the predicatal and minor premises, that Some P1 are not S2; but this information tells us nothing of the relation of S2 to P1 (in that order). [67]
Before we can present and evaluate, by formal means, the conclusion(s) proposed by the Rabbis in such case, we have to find a statement or example which somewhat clarifies the matter, as we did in other cases. The problem, here, is that the statements and examples I have so far come across concerning the present rule are ambivalent[68]. So, we have to proceed in a different manner, and look for an example which, had the Rabbis been more aware of the formal issues involved, they might well have classified under this heading. This proposed approach is admittedly highly hypothetical. For the present research project is not essentially prescriptive, but descriptive; its purpose is primarily, not to tell the Rabbis how they should interpret texts, but to discover how they do interpret texts. We wish to evaluate their methods, not invent methods for them. A value-judgment is ultimately intended, but only after we have something of theirs to evaluate.
Nevertheless, remember, we arrived at our hypothesis concerning the form of shehu kheinyano, not out of the blue, but by a gradual discovery of the forms of the other subdivisions of kol davar shehayah bikhlal veyatsa. Our hypothesis was therefore grounded in Rabbinic practice to that extent, being the only leftover form available. It is, of course, conceivable that R. Ishmael and his successors never had to deal with the situation of compatible (but not subalternative or implicant) predicates in practice, and therefore had no need to develop a hermeneutic response and corresponding rule. This empirical issue is hard for me, personally, to resolve at this time, since I do not have a full inventory of the instances of Rabbinic exegesis at hand. However, I have found a couple of examples in the literature, in which the predicates are objectively in the required relation, even though they are classified differently by tradition (see JL, Appendix 6).
Objectively, these examples should be classed as shehu kheinyano; but traditionally, one of them is classed as shelo kheinyano (rule No. 9, above), and the other as lidon badavar hechadash (rule No. 11, below; but note, regarding the latter example, that it may also be classed as shelo kheinyano, according to how the major premise is read). Thus, the conclusions they yield vary in form. But we cannot, in any case, presume to predict, on the basis of such reclassifications, what the formal conclusions preferred by the Rabbis might be for shehu kheinyano situations; for if they had been aware of the compatibility of the predicates in the suggested examples, they may have proposed other conclusions than those they proposed while unaware. To know for sure, we need an example which is both objectively shehu kheinyano and regarded as such by tradition, which to date I have not found.
The issue must therefore be left open, pending the gathering of more data. That is not a big problem, because, whatever the response of the Rabbis happens to be, we have by now made clear the method by which such response is to be treated: it is to be formalized (substituting symbols for content) and compared to the results syllogistic logic.
We shall now venture some remarks regarding the final clauses of R. Ishmael’s liton toan acher rules, concerning leniencies and severities. Rule No. 9, shehu kheinyano, ends with the phrase ...yatsa lehaqel velo lehachamir (meaning: was singled out to alleviate and not to aggravate); and rule No. 10, shelo kheinyano, ends with the phrase ...yatsa lehaqel ulehachamir (meaning: was singled out to alleviate and to aggravate). Traditionally, these phrases are taken to characterize the result of exegesis, by comparing the general and particular law.
Examples. (a) ‘Alleviation and not aggravation’: Scripture prescribes the death sentence for killing someone, except in a case of manslaughter, for which the sentence is exile instead of death; thus, for manslaughter, the sentence is lighter and not heavier. (b) ‘Alleviation and aggravation’: Scripture prescribes payment of a ransom for his life to the master of an ox which kills someone, except in a case where the victim is a slave; in the latter case, the ox’s master pays the slave’s master a fixed sum (30 silver shekels), whatever the market value of the slave; since the market value of the slave may be more or less than the fixed sum, the latter sentence involves both leniency and severity.[69]
These characterizations have no formal moment, according to our analysis. We cannot predict, on formal grounds, how the general and particular laws, so-called, will compare with respect to leniency or severity. It is clear that such characterizations are essentially ex post facto summaries based on material data[70]. If it so happens that wherever shehu kheinyano or shelo kheinyano exegesis has been used, the results are found to have this or that character, the summaries are true; otherwise, not. It is conceivable that Scripture and Rabbinic exegesis happen to conform to those patterns, but there is no logical necessity that they do. For as far as logic is concerned, anything goes in this respect. This means that the phrases in question do not play a role in getting us to the conclusions; they are technically useless in determining the Halakhah.
With regard to the material issue, I have no direct interest. But it is worth pointing out that R. Ishmael’s said clauses do not seem to be based on complete enumeration, as they ought to be, but on generalization from a few instances. This is suggested by Bergman’s comment concerning shehu kheinyano that “(Although the formulation of this rule states ‘to be more lenient rather than more severe,’ the converse also holds true.) If the item is specified for purposes of stringency, it is not given the leniencies of the general law.” It is also evident, in several Rabbinic examples, that the characterizations are often forced, in an effort to fit R. Ishmael’s statements. Clearly, R. Ishmael based these phrases on overly hasty generalization, from observation of a limited sample of cases. Therefore, they are not only formally unjustifiable, but empirically inaccurate. Consequently, R. Ishmael’s formulations are overly restrictive, in practice.
Nevertheless, let us look further and see whether we can anyway draw some useful information from R. Ishmael’s last clauses, of a formal or methodological sort.
A possible formal interpretation is the following.
If we consider the overall outcome of shelo kheinyano exegesis, what essentially happens is that the major and minor premises are respectively narrowed down and made exclusive, so that the major and minor subjects end up with separate predicates. We could say, loosely speaking, that this result ‘both alleviates and aggravates’, in that, whatever they are, the leniencies and stringencies of the major premise are not applied to the minor term and the leniencies and stringencies of the minor premise are not applied to the major term. Thus, the final clause of R. Ishmael captures the ‘spirit’ of this rule, though not its ‘letter’.
If, now, we turn to the shehu kheinyano rule, and R. Ishmael’s final clause ‘alleviates but does not aggravate’, and we assume that, here too, he was referring to the ‘spirit’, rather than the ‘letter’, of this type of exegesis, we might suppose that the conclusions he would recommend, in situations where subalternative subjects have compatible predicates, are such that the minor premise ends up ‘lighter’ than the major premise. A relatively formal interpretation of this (with reference to a number of predicates), would be that the minor subject ends up with only its own predicate exclusive of the other predicate, while the major subject exclusive of the minor subject ends up with both predicates[71].
I offer this remark very speculatively, without even looking for examples; I very much doubt that that was R. Ishmael’s formal intention. Note that, in any case, some residue from the original text must remain: at least some S1 have to be P1 and at least some S2 have to be P2[72].
Our best bet is a methodological interpretation, which goes as follows. This explanation refers to advice broader in scope than the concerns of deductive or formal-inductive logic.
With reference to shelo kheinyano, we could impute R. Ishmael as saying that, since the major premise has been proven, by ensuing inconsistencies, not to be universal, we must henceforth proceed very carefully and, unless or until otherwise demonstrated, look askance at any other statement we encounter in the text concerning the major term, before extending it to the minor term (through some other exegetic rule). This is reasonable and wise advice. As examples show, such a recommendation does not exclude in advance the possibility that the major and minor terms have some legal predicate(s) in common (they are bound to at least have some non-legal predicates in common, else they would not be subalternative); it only serves to instill caution in the exegetic process.
Our usual epistemological approach is to accept appearances or statements at their face-value, barring reason to deny them; this might be called ‘the easygoing approach’. In the shelo kheinyano situation, however, in view of our having encountered one inconsistency, we have grounds to expect others; so, we would be wise to withhold immediate credulity from subsequent appearances or statements, barring reason to affirm them; this might be called ‘the cautious approach’. These approaches may be analogized to the ways people can be judged: as ‘innocent until proven guilty’ or ‘guilty until proven innocent’. The former gradually excludes certain items (which prove untenable), the latter gradually includes certain items (which prove tenable). In practice, we operate somewhere in the range between those two extremes.
With reference to shehu kheinyano, accordingly, since no inconsistency is implied, the appropriate approach would be ‘easygoing’. Obviously, whatever leniency or stringency is introduced by the minor premise, exempts its subject from incompatible stringencies or leniencies applicable to the major subject in other propositions; but such exemptions emerge from distinct arguments, under the shelo kheinyano rule; so, they are not, properly speaking, a direct outcome of the shehu kheinyano rule. However, residual factors specified or implied somewhere in the text with regard to the major subject, which have not been explicitly or by implication eliminated by the minor premise, may reasonably be assumed to remain applicable to the latter’s subject, unless or until we have reason to believe otherwise.
In this perspective, the phrase lehaqel velo lehachamir, used for shehu kheinyano, is especially intended to contrast with the phrase lehaqel ulehachamir, used for shelo kheinyano, with respect to this issue of methodology.
- Rule No. 11, the last of the principles starting with the common phrase kol davar shehayah bikhlal veyatsa..., completes it with the words ...lidon badavar hechadash, y ata yakhol lehachaziro likhlalo, ad sheyachazirenu hakatuv likhlalo beferush. Translated literally, it says: “anything which was in a generality and came out to be dealt with within a new matter, you cannot return it to its [initial] generality until Scripture returns it to its [initial] generality explicitly”. This rule, albeit superficial appearances is very different from the preceding three. It may be stated as ‘if a member of a certain class, subject to certain predicate(s), becomes a member of a new class entirely, subject to other predicate(s), then again becomes apparently subsumed under its initial classification, it should not recover the predicates of that classification, except in the event that Scripture clearly grants such recovery’. In symbolic terms, this definition says the following:
|
(i) at first, x, an individual, is S1, a subject-class, |
|
and All S1 are P1, a predicate (whence x is P1); |
|
(ii) later, x ceases to be S1 and becomes S2, another subject-class, |
|
and All S2 are P2, another predicate (whence x is P2); |
|
(iii) yet later, x ceases to be S2 and becomes S1 (though No S2 is S1); |
|
(iv) in such eventuality, |
|
though x is (again) S1, it is not necessarily (again) P1, and |
|
though x is not (any longer) S2, it is not necessarily not (any longer) P2. |
A note on terminology, with regard to this rule. It consists of three (compound) premises, with an underlying subject (x), two subject-concepts (S1, S2) and two predicates (P1, P2). We shall refer to the premises as the major (i), minor (ii) and middle (iii), though their conceptual levels are independent; and to the respective subjects and predicates of the major and minor premises accordingly. The (compound) ‘conclusion’ (iv) is a modal statement (of the logical type), forewarning us not to draw certain hasty inferences from the premises.
Let us analyze this situation. We are concerned, here, not with the various classifications of different individuals (extensional modality), but with actual travels of an individual from one class to another and back (natural modality). In the preceding three hermeneutic rules (Nos. 8-10), the issue was how to handle a static situation, where Scripture treats subjects belonging to a subclass seemingly somewhat differently from the way they are treated in the framework of an overclass. The individual subjects are members of the two classes simultaneously; they are not undergoing change, in the sense of becoming, actually ceasing to be one thing and then reemerging as something else. In the present rule, we confront the issue of metamorphosis, which has very distinct logical properties[73]; specifically, the issue is a circular movement: membership in one class, then shift over to a new class, and finally return to the original class.
I derived my reading of the rule from an illustration given by Scherman. Lev. 22:10-11 inform us that common Jews (non-priests) and tenants or hired servants of priests are forbidden to consume ‘holy things’, while servants bought by priests or born in their house may do so. We know (either by a davqa reading of the latter verses, or a qal vachomer from home-born servants, or from an unstated verse) that a priest’s daughter (our symbol, x), whether as a member of her father’s household before she marries a commoner or as the wife of another priest (S1), is permitted such food (P1). Verses 12-13 tell us that it is, however, forbidden (P2) to her (x) while married to a commoner (S2); though if she is thereafter widowed or divorced... and returns to her father’s house, as in her youth (S1), she may consume it (P1). In our example, Scripture happens to explicitly grant reentry of the daughter under the category of priest’s household for the purpose of eating holy things; but the fact that this had to be specified is in itself significant, implying that it could not be simply presumed from the mere fact of her return home (or coupled with a fortiori from v. 11 concerning bought servants, who are newcomers to the household).
In the rule of lidon badavar hechadash, unlike the others, the categories of subject (S1, S2) are not overlapping, they are at variance (they have a common member, x, but at different times); as for the predicates (P1, P2), their mutual relationship is irrelevant, here. The major predicate (P1) applies to our individual qua (in his capacity as, by virtue of) his belonging to the first subject-concept (S1); similarly, the minor predicate (P2) comes to apply to it qua the second subject-concept (S2). With reference to the third premise, a legitimate question arises, was the original subject-class (S1) intended broadly enough to include returnees from an alternate subject-class (like S2), so that the earlier predicate (P1) again applies; or does the later predicate (P2) remain in force (or, perhaps, some third predicate come into play)?
From the point of view of syllogistic logic, granting the premises at their face-value, the general element of the major premise, ‘All S1 are P1’, combined with the final element of the middle premise, ‘x is (again) S1’, would formally yield the conclusion ‘x is (again) P1’. As for the elements ‘x is no longer S2’ of the middle premise and ‘All S2 are P2’ of the minor premise, they do not clarify whether x has remained P2 or is no longer P2 (of course, if P1 and P2 are incompatible, x must cease to be P2; but if they are compatible, the final predicate of x is undetermined). R. Ishmael is clearly aware of these two logical consequences; however, he forewarns us not to blindly follow the first (though, concerning the second, he and formal logic agree).
If we accept the first premise as literally general, our conclusion has to be that the first predicate again comes into force. However, in view of our knowledge that (a) changes of the kind considered do occur in nature and Scripture, and keeping in mind that (b) the intent of general statements in the Torah is occasionally not literal, we cannot presume such an automatic conclusion, and are wise to leave the question open, awaiting Scripture’s answer (directly or indirectly). The literal option is deductive, the anti-literal one is inductive. This hermeneutic rule, instead of advocating some conclusion, preempts any eventual conclusion; its purpose is to ensure that deductive logic is not mechanically used, when the events described take place, unless the text justifies it.
More precisely, according to this rule, if Scripture reiterates the subsumption of the ambulant individual under the major premise (after the said changes), then the major premise’s generality is confirmed; if, however, Scripture fails to do so explicitly, the suggested reaction is, effectively, to particularize the major premise to ‘Not all S1 are P1’. These alternative further proceedings (confirmation or particularization of the major premise) constitute a finite conclusion; so, the process lidon badavar hechadash can be said to have conditional conclusions (rather than merely inhibiting any conclusion).
The above treatment of the rule is different from the traditional, but I think there is no possible doubt that the situation we have described is what R. Ishmael was trying to project. His use here of the qualifier chadash (new), rather than acher (other) as in the preceding two rules, confirms my view, as it suggests actual change of something, instead of a mere intellectual separation between different things. In any event, it would certainly be a wise rule to have; and traditional formulations, as we will now show, do not add anything of practical value to the previous rules and so cannot be appropriate.
If we read this rule as traditionally done, the formalities are indistinguishable from those of the rule shelo kheinyano, if not also the rule shehu kheinyano[74]. But there is no way for formal logic to discriminate between ‘degrees of difference’ between incompatible classes, so that any principle formulated on such basis is bound to be subjectively used. The traditional reading is thus, for all practical purposes, indistinguishable and useless. If we are to assume R. Ishmael to have been saying something meaningful and valuable, the reading I have proposed (based, note well, on an accepted example) seems a better candidate.
It has to be said that the forms ascribed to material cases by the Rabbis are often wrong. Because of their lack of formal tools, the Rabbis often misread the hermeneutic principles; that is, they misplace examples, and since their understanding of the principles is largely based on examples, they are often at a loss to clarify the whys and wherefores of their reasoning processes and to distinguish them from each other. One might have supposed that, since they formulated the principles in the first place, they ought to know more than anyone else just what they mean by them and be free to classify examples under the headings of their choice. But the issue is more complicated than that.
It is evident that the theory and practice of Rabbinic exegesis developed in tandem, over time. The Rabbis observed themselves thinking in a certain manner in certain situations, and subsequently were encouraged to think in the same manner again in other situations. Very often, the similarity between the situations was ‘forced’, and we can see a very artificial effort to jam the example into a mold, to make it fit-in to the desired format[75]. The fact that the formats were themselves rather vaguely defined, facilitated such square-peg-in-a-round-hole antics. But also, we see an uncertainty concerning the opposition of terms or theses: ‘different’ is often confused with incompatible; incompatibility is thought to have degrees; the formal opposition of compounds is not analyzed; and so forth.
All this is further complicated by the existence, in Rabbinic thought processes, of implicit (hidden or not consciously acknowledged) generalizations and exclusive readings, which are just taken for granted. The claim of Sinaitic tradition which gradually developed, and the intimidation it occasioned (the reluctance to question past authorities for fear of rejection by one’s peers), caused the accumulation and perpetuation of such errors, because the process of repeated peer review which normally would uncover and correct errors was considerably inhibited. At best, we can call it incompetence; at worst (to the extent that the authors concerned sensed that they were misrepresenting the principles or contriving the compliance of examples) deception and manipulation.
As a consequence of the various circumstances just described, exegetic acts are wrongly classed, under rule 10 instead of 9 or 9 instead of 10, or 11 instead of 9 or 10, for instances (examples of such misclassification are presented and analyzed in JL. Appendix 6[76]).
Before closing the discussion of the five kol davar shehayah bikhlal veyatsa... rules, I want to again emphasize that my analysis was based on formalization of a limited number of examples. It therefore depends on generalization; for it is not inconceivable that examples exist where the Rabbis have drawn conclusions of objectively other forms than those here encountered (whatever their theoretical claims). Ideally, our study should have been based on comprehensive enumeration of all Talmudic (and post-Talmudic) exegetic acts; such a feat is beyond my reach, since I lack the necessary linguistic tools (Hebrew and Aramaic) and since as far as I know no one has drawn up the required listing (let alone in English) – but I hope someone will one day perform the feat. Nevertheless, what is reasonably certain is that I have formalized the examples available to me accurately, so that we now have an at least partial formal picture of actual Rabbinic thinking processes, enough to formulate a verdict of sorts (comparing the empirical data to Rabbinic pronouncements and to formal logic).
In any case, this research at least has served to establish a clear and sure methodology for the independent audit of Rabbinic harmonization rules and acts. That is in itself a highly important finding, which took time and effort to develop, since no one had done it before and it was not immediately evident.
- Finally, we come to Rule No. 13, which states: vekhen, shnei khetuvim hamakhechishim zeh et zeh ad sheyavo hakatuv hashlishi veyakhriyaa beneihem. This means, clearly, ‘two writings which deny each other until a third comes which reconciles them’. It refers to a situation where we come across two propositions in Scripture, say P and Q, which appear conflicting; the midah recommends we find a third proposition in the text, R, which somehow or other resolves the disagreement between them. Such reconciliation may logically result in neither, or either, or both, the initial two propositions being modified by the third, depending on the role the latter plays:
P and Q remain finally unaffected by R; but R shows that the presumed conflict does not in fact occur in their case.
An example given in EJ: according to Exod. 19:20, “the Lord came down upon Mount Sinai”, and according to Deut. 4:36, “out of heaven He made you hear His voice”. These passages seem to imply that God was both down close to the Earth and up in the heavens; but the apparent antithesis is dissolved, by Sifra (1:7), which alleges[77], with reference to Exod. 20:19, “ye yourselves have seen that I have talked with you from heaven,” that God brought the heavens down with Him when He spoke. Here, the assumption that the heavens stayed in their normal place (up), which was the source of conflict, is denied.
P and Q are finally admitted to be in conflict; but R shows P and/or Q to be more limited than presumed, one or both being in fact conditional rather than (as apparent) categorical, or contingent rather than (as apparent) general.
An example given by Bergman, Num. 7:89 says that “Moses went into the Tent of Meeting” to speak with God, whereas Exod. 40:35 says that he “was not able to enter into” it, adding “because the cloud dwelt thereon”. The latter clause was needed to resolve the contradiction between the first two statements, making them both conditional: Moses came in and spoke with God when the cloud departed, and he stayed out when it was there.
Note the distinct symbolization used in the present rule, in comparison to the other hermeneutic rules: here, we refer to whole propositions (P, Q, R) of whatever form, rather than to propositions of specified forms (as with a fortiori argument or with the preceding rules of harmonization), or to terms (as with klalim uphratim). The 13th rule is the least structured and mechanical of the harmonization rules: we must look all over the text for a premise which is not formally pre-defined, so that our intuitive faculty is more active. Whereas in the other rules, the result is arrived at (for good or bad) more directly and virtually automatically.
The processes involved here are perfectly natural inductive processes, widely used to harmonize apparent divergences in the ever-changing context of empirical and rational knowledge. In natural contexts, they serve to restore consistency when it seems momentarily lost, adducing that either the apparent conflict was illusory for some reason, or that one or both of the conflicting theses were over-generalized or under-particularized or otherwise off-the-mark. In a Scriptural context, it is hopefully the text itself which provides the solution to the problem, informing us of some natural event or specification, or in certain cases a miracle, which modifies our reading of the situation and removes any antinomy.
Note that, according to JE, R. Akiba considered the resolution to be adoption of one of the conflicting propositions, whereas R. Ishmael opted for the view that both are to be modified. But I stress that, formally speaking, there are many possible resolutions, as here specified.
It has to be said that the conflict may not be immediately obvious; often, it is only noticed centuries after the Talmud, sometimes by a picky commentator out to make some point. Also, as originally formulated, the rule of shnei khetuvim predicts that a third proposition, hakatuv hashlishi, will be found in the text to restore the lost equilibrium. However, that is often not literally the case; often, the conflict is actually resolved only by Rabbinic intervention, with reference to a commentary well-established in the oral tradition or by means of a new commentary (with, in many cases, different commentators making different suggestions). In my view, such external intervention requires no special dispensation, since the process, as already noted, is quite legitimate according to generic logic; provided, of course, that it is properly carried out, that is to say, flexibly willing to revise postulates which eventually cause difficulties of their own.
Some commentators (Bergman cites Tosefos Haazarah) have felt a need to justify Rabbinic intervention, and did so with reference to the phrase vekhen, which begins the formulation of this rule by R. Ishmael. They read vekhen as “and, similarly,” and refer it to the preceding rule (No. 12), claiming that the present rule concerns situations where no harmonization is given by the immediate context (meinyano or misofo), and empowers the Sages to decide the issue[78]. However, this attempted justification does not account for the reference to a third Scriptural passage (hakatuv hashlishi). Indeed, according to that view, when Scripture explicitly resolves the conflict, no exegesis has actually taken place, and the rule only refers to situations where Scripture remains silent!
But, in my view, the phrase vekhen could equally well, and more credibly, be read as “and, also,” and taken to refer loosely to all the preceding hermeneutic rules, merely implying that the present rule is the last in the list (or, perhaps, last but not least). When Scripture provides a solution of the problem, it is still exegesis, insofar as we have to find the relevant passage; the rule, in such case, serves to remind us to look for it. As for where Scripture does not seem to provide a solution, why not say that such cases are dealt with using R. Ishmael’s other rules of harmonization. In practice, it is a very fine line which divides the two situations: many allegedly Scriptural resolutions are not automatic, but presuppose a certain Rabbinic reading of the text (e.g. the Sifra reading in the above given example).
The last of the Thirteen Midot is the prototype for the series of rules concerned with harmonization, in that it most clearly depicts the form of reasoning known as dialectic, whose pattern is thesis-antithesis-synthesis[79]. Its hierarchical position is ambivalent. It should, in a way, have been listed first among them, because it is the one most deeply anchored in the text (lidon badavar hechadash has a similar distinction). Before applying any other form of harmonization, we would naturally try to find within the text itself some resolution of the perceived conflict. Failing to find an explicit remark directly or indirectly capable of resolving the difficulty, we might then apply more mechanical procedures, especially that of shelo kheinyano (since lelamed, shehu kheinyano and lidon relate to perceived redundancies, discrepancies, doubts or interpretative tensions, rather than formal inconsistencies).
However, the Rabbis also, apparently, occasionally appeal to the 13th rule to justify more intuitive reconciliations. In that sense, it is also a last resort, and is well placed in the list. If we wish to explicitly acknowledge such reasoning in cases where no Scriptural passage explicitly, or indirectly through one of the other rules of exegesis (assuming them not to be exhaustive), settles the observed difference between two passages, we would have to add a clause to the 13th rule, to the effect that, ‘under those conditions, some credible and consistent reconciling postulate needs to be found’. I think it is fair to say that this added clause has been tacitly accepted and used by all commentators, including R. Ishmael himself. As already said, the pattern of thought involved is natural, and therefore needs no special certification in Biblical contexts, if properly used.
The way certain postulates have come to be preferred to others over time, is simply through the process of peer group review; this consisted in debate among experts to ensure the credibility and consistency of such postulates. That kind of process is, in principle, normal and healthy, effectively a process of collective knowledge development, a garde fou found in every scientific discipline. Of course, peculiar to Rabbinic thinking (and similar enterprises in other religions), are its historically evident authoritarian aspects.
The above comments are based on the data I have for the 13th rule. However, it may be that, with a larger data base, we could formulate the rule with more precision. Among the possible outcomes or alternative theories are the following:
- It could be that rule 13 is concerned, distinctively, with cases where the subjects (or antecedents) of the conflicting propositions are one and the same (or, though different concepts, logically mutual implicants). This is confirmed by the above given two examples; and would distinguish it from rules 8-10, where the major and minor subjects (or antecedents) are subalternatives, and from rule 11, where they are incompatible. In that event, the 13th rule would be defined more precisely, as an argument where ‘All S are P1’ (major premise), ‘All S are P2’ (minor premise), ‘No P1 is P2’ (predicatal premise), whose conclusion consists in denying at least one of those three premises.
- Alternatively, the rule in question may be wider than that in application, and include all cases where the predicates are incompatible (whatever the relation of the subjects). In that event, shelo kheinyano would be a special case of shnei khetuvim hamakhechishim, and the latter would cover additional situations, such as where the corresponding predicatal premise is denied or where the subjects are identical.
- It is also possible that rule 13 was intended to cover, not merely inconsistencies in the strict sense, but in the wider sense understood by the Rabbis, who look upon any discrepancy or redundancy or source of doubt as calling for a harmonizing response of some sort. This outlook was evident in the rules of lelamed, shehu kheinyano and lidon badavar hechadash. In that event, rule 13 would add to rules 8-11 the function of ‘conflict resolution’ by alteration of subjectal or predicatal premises. It might similarly embrace the klalim uphratim rules and others still[80].
We must also keep in mind that, from a formal point of view, the conclusions recommended by the Rabbis in many of the previous rules are not logically necessary. It follows that they are likely to occasionally lead to inconsistencies, and must be regarded as at best tentative. The resolution of such a derivative inconsistency, merely by retreat from the results of application of an unnecessary midah, might have been intended by R. Ishmael as subsumed under the present rule.
Concerning adduction, which we saw (in JL 2) is a Torah-given reasoning process, though one not noticed as such by the Rabbis, nor enshrined by them as a hermeneutic rule. It might be argued that, since adduction is harmonization between conceptual prediction and empirical findings, it belongs under Rule 13. However, to there subsume it, we would have to expand R. Ishmael’s statement, since the latter relates specifically to textual harmonization – it does not discuss confrontations and reconciliations between the Book, or interpretations thereof (by Rabbis or other people), and external reality. Nevertheless, if the rule is adapted, as above suggested, to allow for harmonization by human (at least, Rabbinic) insight, then it may be considered as also including adductive issues.
5.Diagrams for the Midot
Some of the 13 hermeneutic rules of R. Ishmael can be represented graphically, at least in some respects.
- R. Ishmael’s Rule No. 1, concerning a fortiori argument, can be represented by a triangular star, at the center of which is the middle item (R) through which the three other items, P, Q, and S are related to each other.
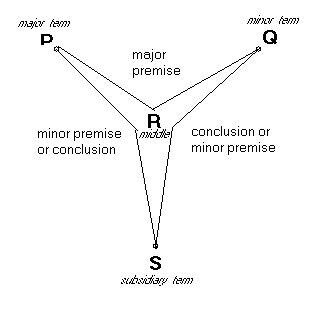
Diagram 8.1
- R. Ishmael’s Rules Nos. 4 and 5, concerning the intended scope of terms, can be represented as follows. In the first case, the intent is narrow; in the second case, the intent is broad.
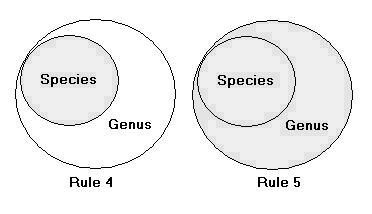
Diagram 8.2
- Rabbi Ishmael’s Rules Nos. 8-9-10, which are some of the Talmud’s harmonization rules, are all concerned with the following logical problem, formulated with reference to the following diagram: knowing the lateral relations between four items (the terms or theses, S1, P1, S2, P2, in the four premises a, b, c, d), what are the diagonal relations between them (i.e. the conclusions, e)?
Diagram 8.3
Such arguments appear much simpler, if viewed as successions of Aristotelian syllogisms (which involved three items, in two premises and one conclusion). They may then be graphically represented, using Euler diagrams. Their formally valid conclusions are then manifest for all to see; and the invalidity of some Rabbinic conclusions is then apparent.
- We suggested (in the previous section) a general formula for the first three (actually, four) of the hermeneutic principles which begin with the phrase kol davar shehayah bikhlal veyatsa.... The first three premises can be individually depicted as follows:
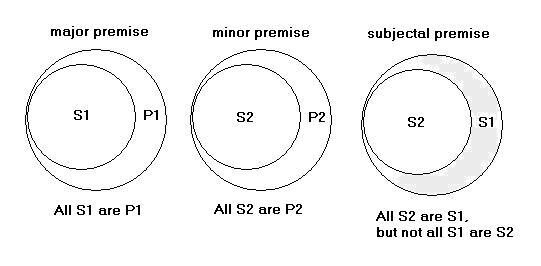
Diagram 8.4
Note that the first two premises leave open the possibility that subject and predicate may be co-extensive, so that the circles labeled S1 and P1 might be equal in size, and likewise the circles labeled S2 and P2 might be one. On the other hand, the relation between S2 and S1 can only be as above depicted, with S2 smaller than S1.
As for the remaining (predicatal) premise and the conclusion(s), we shall consider each case each in turn. But first, let us consider what general conclusions can be drawn from the common premises of all such arguments. Given the major and subjectal premises, we can at the outset, without resort to the other premises, make the following syllogistic inferences and graphic presentation:
|
1/AAA |
3/OAO |
|
All S1 are P1 |
Some S1 are not S2 |
|
All S2 are S1 |
All S1 are P1 |
|
So, all S2 are P1 |
So, some P1 are not S2 |

Diagram 8.5
Note: I did not mention the above 3/OAO syllogism in my original treatment (in the previous section).
It should, however, be pointed out that in the case of Rule 10, since the major premise is particularized in an effort to restore consistency, these initial inferences become annulled.
Similarly, given the minor and subjectal premises, we can at the outset, without resort to the other premises, make the following syllogistic inference and graphic presentation:
|
3/AAI |
|
All S2 are P2 |
|
All S2 are S1 |
|
So, some S1 are P2 |
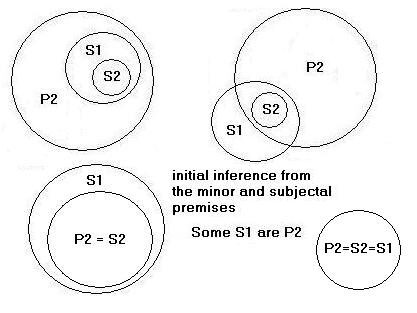
Diagram 8.6
This conclusion is an indefinite particular, note – i.e. in some cases, we may find “All S1 are P2”; and in others, “Only some S1 are P2”.[81]
- R. Ishmael’s Rule No. 8(a) – “lelamed oto hadavar” – the generalizing version of “lelamed”, may be depicted as follows, since its fourth premise is:
All P2 are P1, but not all P1 are P2 (predicatal premise).
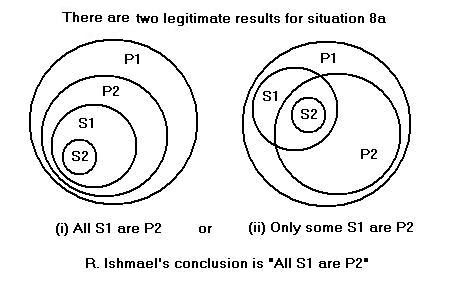
Diagram 8.7
The four premises formally yield the conclusion “Some S1 are P2” (etc.), which is compatible with the two outcomes shown in our diagram.
Rabbi Ishmael concludes (more generally and more specifically) that “All S1 are P2”, which means that he at the outset generalizes the formal conclusion, and precludes the other formal alternative (some S1 are not P2). No reason is given for this hasty action. Thus, note well, although the Rabbinical conclusion is in this case compatible with the formal one, it is not identical with it. Strictly speaking, it is a non-sequitur. The best we can say for it is that it is a legitimate inductive preference to select the more general alternative; however, the Rabbis should remain open to occasional particularization of their conclusion, if it is found to lead to some contradiction elsewhere.
- R. Ishmael’s Rule No. 8(b) – “lelamed hefekh hadavar” – the particularizing version of “lelamed”, may be depicted as follows, since its fourth premise is (note the reversal of order of the terms, in comparison to the preceding case):
All P1 are P2 (predicatal premise).
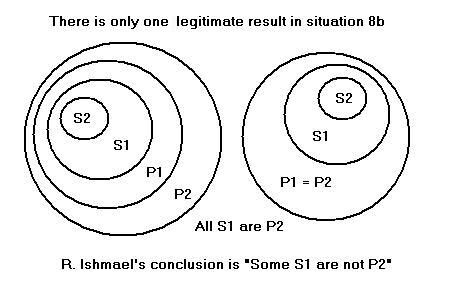
Diagram 8.8
The four premises formally yield the conclusion “All S1 are P2” (etc.).
Yet R. Ishmael draws the very opposite conclusion “Some S1 are not P2”! Why this upside down logic? Apparently, he mentally considers the premises in conflict, due to some perceived redundancy in the text, and seeks to harmonize them by excluding all S1 other than S2 from being P2. But such particularization is logically illegitimate, since there was in fact no formal conflict between the premises, and textual repetitions can hardly be considered as such. Judge for yourself.
- R. Ishmael’s Rule No. 10 – “shelo kheinyano” – is difficult to depict since it concerns a conflict resolution. Its fourth premise is:
No P1 is P2 / No P2 is P1 (predicatal premise).
As the following first diagram shows this premise is in conflict with the others, since if the circles representing P1 and P2 cannot overlap at all, then the circles S1 and S2 cannot satisfy all the given conditions regarding them. The problem can be faced in a number of ways:
- That is, if S2 is wholly in S1, and S2 is wholly in P2, then S1 cannot be wholly in P1. We could accept this and propose that S1 is partly in P1 – and partly (to an extent at least enough for S1 to cover S2) in P2.
- Alternatively, if S2 is wholly in S1, and S1 is wholly in P1, then S2 cannot be wholly in P2. We could accept this and propose that S2 is partly in P2, and partly in P1; but if we say so, we must also assume S2 is not entirely (but only partly) within S1.
- We might also resolve our dilemma by assuming S1 and S2 not to at all overlap, like P1 and P2.
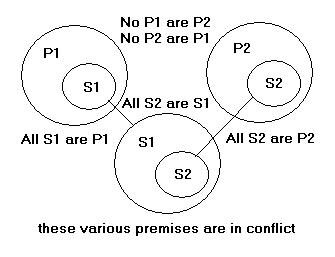
Diagram 8.9
R. Ishmael’s preferred option, for resolving the conflict dealt with by Rule No. 10, seems to have been (a). That is, he kept the subjectal and predicatal premises, and even the minor premise, unchanged and chose to tinker only with the major premise, concluding: “Some, but not all, S1 are P1”. Diagrammatically, this Rabbinical resolution of the conflict looks as follows:
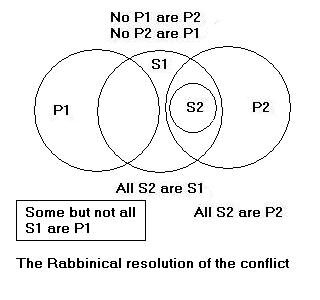
Diagram 8.10
This is a formally acceptable option, even though not the only conceivable option. That is, though the Rabbinical response is not per se in error, it should be kept in mind by them that other inductive responses are possible if the need arise, i.e. if this response later prove undesirable for some reason.
- R. Ishmael’s Rule No. 9 – “shehu kheinyano” – presumably has as its fourth premise:
Some P1 are P2 and some P1 are not P2, and
some P2 are P1 and some P2 are not P1 (predicatal premise).
This situation, where P1 and P2 only partly overlap, may be graphically represented as follows:
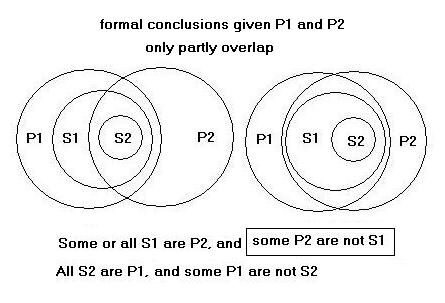
Diagram 8.11
The conclusions we can formally draw are obvious enough. Since “Some S1 are P2”, as well as, “All S2 are P1” and “some P1 are not S2”, are general conclusions possible from the first three premises, without resort to the predicatal premise – the only formal conclusion specific to the current predicatal premise is “Some P2 are not S1”.
It is not clear (to me so far, at least) what R. Ishmael proposes to conclude in such cases.
- R. Ishmael’s Rule No. 11 – “…lidon badavar hechadash” – can also to some extent be represented graphically. Do not refer in the present case to the earlier common premises and conclusions (for Rules 8-10) – this is an entirely different situation. Here, we are initially given the premises:
All S1 are P1 and All S2 are P2
And we are told that an individual, say ‘x’, changes over time from membership in the class S1 to membership in the class S2. Whence, incidentally, by singular syllogism, x is initially P1 and later P2. Later still, x leaves S2 and returns to S1. Formally speaking, granting the given premises constant, there is no doubt as to the outcome of such return: x must again be P1. As to x’s relation to P2, it depends on further conditions; for we are not told in the way of a general premise whether P1 and P2 overlap or not.
These formal considerations are illustrated in the following diagram (assuming here, for the sake of argument, that P1 and P2 are mutually exclusive):
Diagram 8.12
However, R. Ishmael conceives the possibility that when x returns from S2 to S1, the relation of S1 to P1 may in the meantime have changed to “Only some S1 are P1”, so that we can no longer syllogistically infer from x being S1 that x is P1.
Alternatively, the original premise “All S1 are P1” may have from the start been less general than apparent; that is, it may have more specifically been intended to refer to “All first-time members of S1”, so that we cannot be sure whether P1 applies “returnees to S1” like x.
Thus, the preceding diagram might conceivably be revised as follows:
Diagram 8.13
Anyhow, R. Ishmael considers the issue open, and recommends the matter be verified in the Biblical text.
- R. Ishmael’s Rule No. 13, the last in his list, covers many different cases, most of which cannot readily be illustrated. However, the following diagram illustrates one example of the dialectic often involved, where thesis and antithesis are both narrowed, and replaced by their synthesis or common ground.
This illustration is symbolic, note well, because strictly speaking (in class logic) the propositions “All S are P” and “Only some S are P” should overlap – and their common ground, the indefinite “Some S are P”, would be their area of overlap.
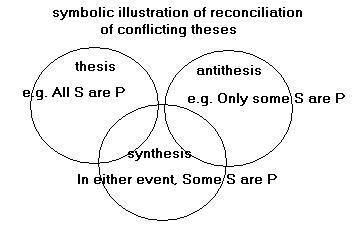
Diagram 8.14
This is just one example – the most ‘deductive’ – of how these conflicting theses might be reconciled. Other inductive possibilities would be to asymmetrically favor one or the other given theses – in which case, the selected one would constitute our synthesis.
In some (other) cases, too, it is possible to argue that the theses are not in as real a conflict as at first appears.
Drawn from Judaic Logic (1995), chapters 10-11.
[1] The present analyses were made possible thanks mainly to Bergman's detailed presentation of the 13 Midot. Though I dislike that author's pompous tone and unquestioning fanaticism, and disagree with many of his specific positions, he is to be commended for his unusual efforts to clarify the hermeneutic principles. All too often, authors are simply content with listing examples with a minimum of reflection; he at least tries (if not always successfully) to sort out logical relations explicitly.
[2] The formalization of relations is not technically valuable (apart from saving space), and tends to alienate and confuse readers; for these more abstract features of propositions, we shall stick to ordinary language.
[3] We may regard the Rabbinic principle ain mikra yotse miyedei pheshuto (quoted by EJ, p. 371, with reference to Shab. 63a and Yev. 24a, and there translated as "a Scriptural verse never loses its plain meaning", with the added comment "i.e., regardless of any additional interpretation"), as an implicit recognition that interpretations using the hermeneutic principles were not always natural. It may be asked how they managed to mentally accept conflicts between a midah-generated reading and a simple reading (pshat), given such a principle!
[4] I am referring here to the Rabbinical subdivision of the dayo principle discussed in a footnote to JL 4.4.
[5] Notwithstanding, the Sages were, in my view, very wise to reject corporeal punishment for breach of prohibitions discovered through qal vachomer argument, or for breach of Torah prohibitions whose penalties were inferred through qal vachomer argument. In practice, we can rarely if ever be 100% sure of having freed our deductions of all possible material uncertainties; and therefore some injustice might be caused. What is true of qal vachomer, the most deductive of Talmudic arguments, should be all the more true of the other hermeneutic principles. (According to EJ pp. 371-2, this canon concerning inferred prohibitions or penalties, is R. Ishmael's: ain oneshim min hadin; R. Akiba disagreed. We are referred to J.T. Yev. 11:1, 11d.)
[6] We are not here dealing with a dead language, so the job is less difficult.
[7] e.g. does 'take' (qach) always signify acquisition by monetary payment, or must other meanings of the term be supposed, and if so how are they to be distinguished? It is not enough that an analogy is applied in one instance (without problems ensuing from that one application); it has to be tested in all other cases where the term appears, throughout the text at hand.
[8] The references given by Bergman for these three provisions are all post-Talmudic: Halichos Olam for the first two, and Rabbeinu Tam and Tosafot for the third.
[9] Or, to be more explicit: pretensions, lies – made in support of a certain ideology, that of unchanging oral law. Note well the basis of my accusation: precisely in the attempt to buttress their concept of the fullness and continuity of tradition, these people are forced to acknowledge the occurrence, in the case under consideration, of incomplete transmission of information, and thus imply a loss of data in the interim and the unreliability of the transfer. The proposed formulae are therefore inconsistent with their own motive, and therefore must be inventions.
[10] EJ, p. 368, refers us to Shab. 64a and J.T. Yoma 8:3, 45a. EJ explains the development of the idea of "free" (mufneh) terms, as a way to prevent abuses of gezerah shavah in the schools; it adds that this is a R. Ishmael requirement, which R. Akiba apparently disagreed with.
[11] Not to be confused with the principle of R. Akiba that in the Torah no word is superfluous and no word-placement is accidental.
[12] Note, however, that in some cases, traditionally classed as heqesh (see Abitbol, pp. 100-104), Scripture itself explicitly establishes the parity between the two areas of law. For instance, Deut. 22:26, which compares rape and murder, saying "for as when... even so..." (ki kaasher... ken hadavar hazeh.). In such cases, an inference is much more certain, though it may well have some limits, because it is analogical rather than contextual.
[13] JL, Addendum 6.
[14] Heqesh and semukhim are classified by commentators with gezerah shavah; but I am not sure why (except for analogies given explicitly in the text) – they are not really subcategories of it, being based on neither homonymy nor synonymy, but on textual proximity. Perhaps it is because they often involve elements of gezerah shavah, that they were rather grouped with it. Also note, the distinction between them is ambiguous: in text originally devoid of punctuation, like the Torah, how to tell the difference between the two parts of the same verse or two touching verses? It only becomes meaningful once the subdivisions of the text are established.
Looking further into the issue, I found some interesting remarks in J.E. Apparently, gezerah shavah initially referred to "analogies in either word or fact", but eventually was restricted to verbal analogies (homonymies), while heqesh became used for factual analogies (synonymies). If that is true, my presentation of these terms, based rather on Bergman's account, is inaccurate (terminologically, though not in essence). With regard to semukhim, it is attributed by J.E. to R. Akiba, quoting him as saying "every passage which stands close to another must be explained and interpreted with reference to its neighbor" (with reference to Sifre Num. 131); it adds that 'according to Ishmael, on the contrary, nothing may be inferred from the position of the individual sections'. In view of this, semukhim cannot strictly-speaking be counted as implicitly included in the 13 Midot of R. Ishmael.
[15] A case in point seems to be the above given example (Exod. 20:13): supposedly the next two commandments (against bearing false witness and coveting) are not subject to death penalty; in that case, why should stealing (or kidnapping) be a capital offense? Of course, if a proposition is surrounded on both sides by a certain subject-matter, it becomes more likely that the common subject-matter of the two adjacent propositions somehow concerns the boxed-in proposition. Nevertheless, the possibility of accidens remains; there may well be significant underlying differences, which can be pointed to. An example is Exod. 21:15-17, where a law concerning kidnapping is found between two laws concerning striking and cursing parents, respectively. (Note that, as an acquaintance of mine, Dr. M. Izbicki, has pointed out, the laws on striking of parents and kidnapping both concern violent acts. Also, see Cohen, p. 474; the law assigns a penalty of strangulation for these two, but stoning for cursing parents).
[16] Regarding heqesh and semukhim, Bergman adds additional details, which we will not comment on, here, to avoid repetitions. I want only to point out that the semukhim inference he gives as an example at the end of the section is very odd: from (Deut. 22:11) the proximity of the prohibition of 'shatnez' and the prescription of 'tzitzit', the conclusion is drawn that shatnez is allowed in the case of the tallit! This is far from normal inference, since the conclusion is an exception to one of the premises, although there was no inconsistency between the premises. Formally, the argument runs as follows: 'You mustn't do X. You must do Y. Therefore, when you do Y, you may do X'. Since the conclusion formally implies 'you may do X' it is contradictory to the major premise; such argument thus depends on an anti-literal particularization of the major premise.
[17] Our identification of binyan av with causal arguments may be too narrow; some examples in the literature seem like mere extrapolations with nary an underlying cause and effect thought-process (though we might construct one, ex post facto). An example given by Scherman illustrates this: Just as one may neither marry one's sister from the same two parents, nor one's father's full sister; then, since one may not marry one's sister from the same mother but different father, 'it follows that' one may not marry one's father's maternal half-sister (ref. to Yevamos, 54b). Scherman says binyan av is also known as mah matsinu? ("what have we found?"), though Bergman informs us that these two were counted separately in Hillel's list. I suspect the Rabbis at first engaged in generalizations with little reflection, and then gradually found it necessary to clarify conditions.
[18] English logician (1806-1873), author of A System of Logic (1847). Mill's formulation of these methods is more complicated than the one proposed here: 'agreement' is observed constant conjunction of two phenomena, 'difference' is the constant conjunction of their negations; thus, the formal relationship is mutual, i.e. the same in both directions: this is the strongest form of causality, in which the cause is not only sufficient for the effect, but necessary or a sine qua non for it. Note that, in all such definitions (as Mill was aware), cause and effect are difficult to distinguish: to do so, we must look at their temporal or conceptual sequence. Note also that Mill suggested other important methods, namely 'residues' (elimination of alternatives) and 'concomitant variations' (see my The Logic of Causation, Appendix 1).
[19] This approach is known as Chada mechada (Aram., 'one from one'). If the one-verse variant is so called, then the two-verse variant may presumably be called 'one from two' (but I do not know what it was actually called).
[20] According to Bergman, this second school claimed the one-from-one inferences obvious and not needing to be included in the 13 Midot. How they viewed the 'one from two' formula, he does not say.
[21] Heb. tsad hashaveh.
[22] Added proof of which is the lack of distinction, in the 'common feature' approach, between one-verse and two-verse inference in accordance with R. Ishmael's formula. That is, if in this approach 'one-verse' means 'one from two', then what might 'two-verses' mean?
[23] Logicians refer to the underlying logical fallacy as post hoc ergo propter hoc (i.e. 'after this, therefore because of this').
[24] Unless, of course, it is already proven that A, C, D are the only alternative possible causes of B; so that the inference consists in elimination of two out of three possibilities. But that is not everywhere the case.
[25] The logical naivety of such argument should be obvious. Say a boss calls three of his employees to his office (intending, say, to congratulate the first for his new-born son, give a raise to the second, and fire the third). No one knows the boss's reasons, but the third employee tries to guess why he has been invited, by looking for a 'common factor' in the two others. He says: "it cannot have to do with hair colour for the first is blond and the second is a brunette; it cannot have to do with honesty, because the first is dishonest and the second is honest; it must therefore have to do with nose shape, because both, and indeed I too, have the same nose shape." His whole argument is utterly fallacious and beside the point!
[26] For it always remains conceivable that non-mention of B in certain passages signifies negation of B, even though there are no known cases of presence of A with absence of B, which fact inductively allows us (indeed, obligates us) to generalize and say that A implies B.
[27] According to the History of Philosophical Systems, p. 67, hermeneutics for purposes of Halakhah consist of “strict logical rules”. I quote this here quite incidentally, to show how far the myth of a Rabbinic logic is spread.
[28] The assassination of Y. Rabin comes to mind.
[29] JL. Addendum 7 (part).
[30] Conditional/partial causes, considered together with their conditions or allied parts (i.e. collectively), constitute unconditional/complete causes. Occasional effects, in loosely defined surrounding circumstances, become constant effects, when the significant circumstances are more precisely pin-pointed. All such variations on the theme of causality are obvious to anyone who has studied hypothetical logic, considering multiples and compounds of antecedents and consequents, and nesting; it is no great secret (at least nowadays).
[31] Where X, Y, Z have in common A, and X, Y have in common B; and they would conclude that Z has B, also.
[32] It does not surprise me, therefore, that, according to Bergman, 'the Gemara does occasionally raise such a refutation'. He adds that 'the commentators (to Kesubos 32a) have formulated principles to explain these exceptions'; I have not seen these principles, but we must keep in mind that they are ex post facto rationalizations, since natural logic allows alternative causes.
[33] Another issue they raise is whether the exceptions have to be 'significant' or not – claiming that refutation of a 'one from one' binyan av requires a legal exception ('stringency or leniency'), whereas against a 'one from two' binyan av, any exception (legal or non-legal) will do. I can only say that such a distinction is not made by natural logic.
[34] I refer here, of course, to deductive logic; if the 'implication' is merely inductive, i.e. not necessary but only recommended as probable, it might conceivably be preempted with reference to wider considerations.
[35] See also, possibly, the items: exegetical principles, 2 references; rules by which law is expounded, 2; texts, exposition of, 3; texts, implication of, 1.
[36] This phrase is wrongly translated by Bergman as "generalizations and specifications"; we would prefer "generalities and particularities" or "genera and species". Strictly speaking, the term generalization, in English, refers to a mental process moving from a particular statement to a general one, and specification refers to a movement from a vague statement to a more precise one. Here, however, the issue is finding out how wide or narrow was the intent of the writer of the text.
[37] Note, however, that in English an adjective usually precedes a noun, while in Hebrew if follows it.
[38] A way to explain the mention of the overclass is to regard it as intended to allude to its instances or subclasses not included in (or alluded to by) the mentioned subclass; which are to be the subject of an unstated proposition of opposite polarity, which makes the stated particular a contingent.
[39] Albeit the theoretical formal convergence between these approaches, they in practice often led to divergent material conclusions (with R. Akiba's often ending up as Halakhah). I would need more specific knowledge of the Talmudic debates concerned to be able to explain why. But, assuming I have correctly understood the formalities and basing myself on the few cases I have studied, I would say that such differences simply go to show the amount of subjectivity involved in the 'inferences', in practice.
[40] e.g. 'logical arguments, syllogism, adductions, are means to knowledge' does not restrict the genus to the listed species. One might construct a sentence in this way, if one thought some auditors unable to grasp the generic subject's name without apposition of some more familiar species names.
[41] e.g. 'Aristotle's syllogism, a deductive argument, yields categorical conclusions' does not intend the genus as a whole but only the species. The genus, here, serves only to place the specific subject in a larger context.
[42] It is interesting to note that the rationalistic philosophy, trying to explain every word and word placement in a certain preconceived manner, which is assigned to R. Akiba, is here, and in other instances, really at the basis of R. Ishmael's inferences, as well as R. Akiba's.
[43] It is noteworthy that R. Ishmael mentioned only the first of these as one of his rules, ignoring the second and also klal-klal-prat and prat-prat-klal. My explanation of such repeated gaps in R. Ishmael's list is simple: as often in the early stages of an investigation, thinkers do not initially work out an exhaustive analysis of the topic concerned with reference to symmetries, but rather concentrate on cases which happen to arise before them in the context of their less abstract concerns. It is only later that they, or their successors, look into other possible combinations and permutations suggested by reshuffling the terms at hand. R. Ishmael did not get around to that systematizing stage; his successors did. (All well and good; what is annoying is their attempts to justify their results by imputing them anachronistically to him.)
[44] A technical distinction suggested by the Rabbis between the two stated principles is that, quoting Bergman, the first "dictates that every item which bears even one similarity to the specification is included," whereas in the second "the item to be included must resemble the specification in at least two aspects." He adds: "How significant the resemblance had to be was left for the Sages to determine. Occasionally, they considered several aspects as one." Here again, I must say, I see no natural basis for these added details.
[45] These words are variously understood by the Rabbis.
[46] Another kind of example is Num. 18:16, which according to Bergman is interpreted in Shevuot 4b as klal ukhlal uphrat. Here, the forcing consists in reading a subject, predicate and qualification of predicate as classes (broad, broader and narrower), ignoring entirely their relative positions (logical roles) in the sentence.
[47] Why he should do so, when he separated klal uphrat and prat ukhlal, is a mystery to me; or alternatively, why were not the latter two and their multiples grouped together, similarly? I would suggest, here again, a failure to stand back from accumulated knowledge and re-order and systematize the results obtained.
[48] For instance, the example from Lev. 1:2 given earlier would, according to Bergman's definitions, constitute a klal hatsarikh liphrat rather than a klal uphrat, as well as I can tell. Note, however, that Bergman hints that 'there are many varying opinions' concerning the definition of hatsarikh processes; so, we might reserve judgment.
[49] This distinction is reminiscent of that which logicians make, between categorematic and syncategorematic terms, though not exactly identical. Note that, unlike independent terms, dependent terms are not conjoined by a mere 'and', but by more intricate relations like 'of', 'by', 'for', 'through'.
[50] A Torah example might be Num 18:16: "according to your valuation, five silver shekels" (mentioned in an earlier note), where 'five silver shekels' makes no sense by itself, apart from the concept of 'valuation' (in this case, for redemption purposes).
[51] It should be noted, however, that certain terms, which are colloquially put in a similar format (notably, 'capabilities of' and 'metamorphosis of') cannot be freely permuted without causing eventual contradictions. But such issues cannot be addressed in so narrow a context; they are fields of logic in themselves.
[52] A case in point was indicated in an earlier footnote (to 8.2): the inference, from the prohibition of shatnez and the prescription of tzitzit, that shatnez is allowed in the case of the tallit. But also, previously and further on, we find many tacit inferences in Rabbinic thought, which though allied to explicited principles, are not themselves aspects of those principles.
[53] Though possibly "text, superfluous", which has only one reference, applies.
[54] Note that these rules differ from the klalim uphratim in that, rather than concerning the mutual impact of terms, they concern the mutual impact of propositions, estimated by careful scrutiny of the subjects and predicates they involve, as well as their various other formal features (polarity, quantity, modality, etc.).
[55] Note carefully that it is the narrower subject S2 that implies the wider subject S1; for that reason, we say that S1 is subaltern to S2. On the other hand, since S1 includes S2, we say that S2 is subordinate to S1.
[56] If two propositions have identical (or at least, logically implicant) subjects (both S, say), these rules do not apply. In such case, we are dealing with ordinary 'oppositional logic', so that the opposition of the propositions is in principle identical with the opposition of the predicates. However, if the quantity differs in the two premises, then it might be argued that their subjects are not technically equivalent, but merely subalternative (all S = S1 and some S = S2). Whether in the latter case the Rabbis would apply the rules in question, I do not know.
[57] Actually, I realized later, one more inference is possible. This is shown in the next section.
[58] Frankly, in my view, the davqa reading would seem the more likely of the two (though not inevitable), because that would immediately explain why Scripture did not simply say 'All S1 are P2'.
[59] Note in passing that Scherman (p. 51) uses the same area of the text to illustrate the first variant of lelamed. From Lev. 7:19, which allows the ritually pure to eat [sacrificial] meat (and, therefore, supposedly, granting an exclusive reading of the text, forbids the impure from doing so), and v. 20, which decrees a penalty of karet for an impure person who eats peace-offerings, he infers the same penalty for all [holy] offerings. It is interesting that this sweeping conclusion is in disagreement with Bergman's more nuanced result obtained by means of the second variant of lelamed! I do not know which of them is considered Halakhically correct. However, my reading of v. 19 is that it refers to peace-offerings, since not only the previous verse but the two after concern these offerings, in which case Scherman's argument is not really a first-variant lelamed, but simply a generalization from peace offerings to all offerings (which does not mean Bergman is right, of course).
[60] By definition, every species is in some respects different from, as well as in some respects the same as, other species of the common genus. In practice, the Rabbis rather arbitrarily propose divisions, without adductive control.
[61] If more than two concepts are involved, we can easily reduce them to two. Thus, for instance, if X = 'a + b + c' and Y = 'a + b', then 'a + b' are effectively one concept and 'c' the other, for our purposes. However, note well, if there is, as well as a missing element in one of the compounds, any explicit incompatibility within them (for instance, X = 'a + b + c' and Y = 'a + notc'), then they (i.e. X and Y) are automatically contrary.
[62] Note that, granting 'a' to be true, 'a+b' and 'a+notb' are no longer merely (indefinitely) incompatible, but become contradictory (i.e. not only they cannot be both true at once, but they cannot be both false at once).
[63] The decision depends, in part, on the known relationships between the elements 'a' and 'b'. They must be compatible, since 'a+b' occurs, in our situation. If 'a' implies 'b', then 'just a' implies 'a+b'. In all other cases, the combination 'a+notb' remains logically possible, though in some cases it may be materially absent or even impossible, for natural or Scriptural reasons.
[64] However, the situation of shehu kheinyano can indeed be predicted in a wider perspective, which consists in defining the two predicates, initially, as P1='a' and P2='b', then considering the logical possibilities of conjunction between the various combinations of a, b, and their negations. For P1 may equal 'a+b' or 'a+notb' or 'a+b or a+notb', while P2 may equal 'a+b' or 'nota+b' or 'a+b or nota+b'. These 3+3 combinations (of which 2 are disjunctive) imply nine conjunctions. Of these conjunctions, five are between incompatibles (shelo kheinyano), and four are between compatibles; of the latter, one yields 'P2 implies P1' (lelamed oto hadavar), one yields 'P2 is implied by P1' and one yields 'P2, P1 imply each other' (lelamed hefekh hadavar), and, finally, one (namely, the conjunction of the two disjunctions) admits of 'P2 being unconnected or subcontrary to P1'. This last case allows for shehu kheinyano.
[65] We cannot go into the complex proof of this principle here. It has to do with factorial analysis (see my work Future Logic on this topic).
[66] This is not a very good example, in my view, since the text describes the slave as possibly having a wife (implying him a male), and concerning the maid-servant says "she shall not go out as the men-servants do" (referring apparently to the preceding verses concerning the Hebrew slave), so that the subjects obviously do not overlap and the proposed inference is unnecessary. I wonder, too, if female thieves are sold by the courts; in any event, the daughter is not sold by the courts. However, ignoring all that, we may use the differing laws of release as a partial illustration. Better examples are given further on.
[67] For the record, note also that, in the case where P1 and P2 are subcontrary, nothing more can be deduced from the given premises.
[68] An acquaintance of mine, Mr. S. Szmerla, pointed out to me, when I asked him for examples, that it is quite possible that some of the hermeneutic rules have only one or two actual instances. It is therefore not at all sure that we will find a sample, which is recognized by both the Rabbis and logicians like me as shehu kheinyano. A systematic listing and analysis of all exegetic acts in the Talmud is highly desirable, evidently.
[69] Example (a) is from Scherman. Example (b) is Abitbol's. However, it should be clear that, in the latter example, the focus of comparison is incorrect: we should not be comparing the fixed sum to the market value of the slave (as Abitbol does, following tradition, presumably), but to the ransom for the ox master's life. If the ransom for a free man's life is uniformly greater than the fixed sum for a slave, then the law for the slave case 'alleviates but does not aggravate'. If the ransom may be greater or smaller than the fixed sum, then we might say the fixed sum 'alleviates and aggravates', in this sense (instead of Abitbol's). Another criticism: in any event, none of these interpretations allows the phrase 'alleviate and aggravates' to be used; the accurate rendering would have to be 'alleviates or aggravates', judging by this traditional example. However, this may be judged an issue of translation, since 've-' is in other contexts read as 'or' as often as 'and'. All that goes to show the approximativeness and unreliability of Rabbinic thinking.
[70] Another example worth noting. Concerning the Hebrew slave and maid-servant case, considered earlier: Scherman explains that the maid-servant benefits from certain leniencies and stringencies denied to males, such as that she may go free even before six years of service and her master can betroth her against her will. But, I say, these differentia are given by the text, they are not outcomes of exegesis; it would change nothing to the reasoning process if there were only comparative leniencies or only comparative stringencies, so long as at least one pair of predicates was incompatible.
[71] A more material interpretation (ignoring Bergman's above-mentioned comment), would be the following. If P2 is more lenient than P1, then people in group S2 should not receive the greater burden of P1, but remain P2 only; while the rest of those in group S1 may remain P1 only, or be both P1 and P2; this is the most fitting case, of course – probably just what R. Ishmael had in mind. However, if P2 is more stringent than P1, then either people in group S2 should have their burden decreased, by being both P2 and P1, while the rest of those in group S1 remain P1 only; or alternatively, people in group S2 remain P2 only, while the rest of those in group S1 should have their burden increased, by being both P1 and P2; but in either of these cases, note, the burden of S2 people is still greater than that of the rest of S1 people, at the end. (Taking Bergman's comment into account, the predicates in the latter event would be kept separate, as in the former case.) It is evident, in view of the multiplicity of possible hypotheses, that R. Ishmael's phrase 'alleviates but does not aggravate' is very ambiguous, and therefore no sure guide.
[72] This is true in all exegesis: it is granted by the Rabbis, who said ain miqra yotse miyedei feshuto ("a Scriptural verse never loses its plain meaning", EJ referring us to Shab. 63a, Yev. 24a). In formal contexts, 'simple meaning' refers to the minimum necessary implication of any proposition, namely an indefinite particular.
[73] See our logic primer, JL 1.2.
[74] The traditional reading of shehu is formally indistinguishable from shelo; so, in that reading both are indistinguishable from lidon badavar hechadash. But if we read shehu as concerned with compatible predicates, as I do, then it is not comparable to the traditional reading of lidon.
[75] This effect is sometimes achieved by passing over some relevant detail in the written text, as we see in an example given further on. We might regard this as a non-formal issue; or refer to it as a failure to take into consideration the full context of information available. There are no doubt other ways 'molding' occurs. The reason for this practice is that it 'legitimizes' an argument, gives it a semblance of being traditional.
[76] I apologize to readers for going into such detail, but it is necessary, to substantiate my serious accusations. I hope one day someone takes the trouble to analyze all extant Rabbinic arguments in equal, and indeed greater, detail; it bothers me when people get away with fallacious reasoning. It should be clear that it is not the content that concerns me, I do not care what the Halakhic outcome is; what is important is that the process be valid.
[77] The reading in Sifra is by no means that I can see obvious; so, this is not an example of Scriptural reconciliation, but merely one of Rabbinical reconciliation. See further on.
[78] In other words, according to this view, rule No. 13 concerns, not explicit (meforash) reconciliations, by the Torah itself, but implicit (satum) ones, by the Sages. Bergman adds, characteristically, "and the Torah requires us to follow their determinations", but he does not state where it does so.
[79] With regard to this three-word description of dialectic, the following is worth noting. At first sight, "thesis" and "antithesis" refer to the two ideas in conflict, and "synthesis" to their reconciliation. But we could also say, upon reflection, that "thesis" refers to both the ideas in conflict, "antithesis" to the realization that they are in conflict, and "synthesis" (as before) to the resolution of the conflict.
[80] For instance, the weird semukhim argument, offered by Bergman (see earlier footnote of the present chapter), might be regarded as a "resolution of conflict" of sorts (though one of very doubtful validity).
[81] Quite incidentally, I notice while writing this that in Future Logic (p. 37), I state that the mood 3/AAI is a derivative of 3/AII; but it could equally be derived from 3/IAI. Similarly, 3/EAO could be derived from either 3/EIO (as stated) or 3/OAO.
